Вопросы теоретической геологии.
6. О форме золотин в россыпях.
В.П. Макаров, А.В. Сурков.
Российский государственный геологоразведочный университет, Россия
При проведении различных литологических исследований широко использовался ситовой гранулометрический анализ рыхлых осадочных пород [5, 7, 8]. В качестве развития и совершенствования этого метода был создан новый метод исследования осадочных пород– грануло–минералогический (далее МГМ), основанный на измерении размеров и веса каждого зерна породы [6, 9, 10, 11] из проб рыхлых отложений. Метод не нов, попытки его использования совершались еще в 40-х годах ХХ века, но только А.В. Сурков стал проводить его в массовом порядке, что позволило собрать громадный материал и сделать некоторые обобщения. Изменение подхода к анализу зерен, переносимых водными потоками, позволило получить новую информацию об особенностях формирования механогенных пород [6]. Далее результаты применения методики А.В. Суркова заимствованы нами для оценки свойств зерен золота, или золотин, в россыпях.
Для решения задачи использованы результаты измерений параметров (вес в мг и размеры в мм по осям А, В и С) золотин песчано- алевритовых фракций (0,01- 2,5 мм), проведенные в разные годы А.В. Сурковым (МГРИ) и опубликованные в [6, 10, 11]. Далее ссылки на эти работы не делаются. Эти данные - средние значения из выборок, содержащих более 100 – 200 зерен, свидетельствуя о статистической представительности полученных выводов. Наша задача состояла в анализе особенностей поведения золотин. Для решения задачи выявлялись связи между параметрами золотин путем построения диаграмм, на осях координат которых откладывались размерные и весовые параметры золотин. Виды связи определялись через определения параметров выявленных линейных уравнений первой степени. При кинематическом анализе будет анализироваться поведение зерен простого класса [2] с использованием представлений о типоморфизме зерен, т.е. зерен, относящихся к одному типу в морфологической классификации, и принципа регулярности. Эти понятия описаны в [3].
РЕЗУЛЬТАТЫ ПРОВЕДЕННЫХ ИССЛЕДОВАНИЙ.
А. Взаимосвязь плотности и размерных параметров. В табл.1 приведены результаты измерений размеров золотин, а на рис. 1- график их зависимости; распределения параметров золотин с высокими коэффициентами корреляции (R2) описывается уравнением V= 0,0533Р + 0,000699 (R2 = 0,987). Это уравнение соответствует вычисленной плотности золота ρ= 18,76 (истинное значение ρo =18,2) и отражает высокую близость рассчитанных значений ρ к эталонным параметрам, т.е. k » 1. Все пробы золотин (табл. 1) относятся к одному множеству типоморфных зерен призмоидного типа. Подобные зависимости выявлены и для других россыпей Дальнего Востока, отраженные в таб. 2. В ней уравнение P = ρV + A отражает вид этой связи, причем параметр ρ равен виртуальной плотности золотин, находящихся в выборке. На рис. 2 и 3 приведены некоторые диаграммы по этим объектам.
Полученные материалы позволяют сделать следующие выводы.
1.С высокими значениями R2 точки распределения параметров золотин в координатах (А, В) приурочены к прямым линиям, свидетельствуя о принадлежности их к одной типоморфной группе. Рассчитанные значения ρ золотин часто ниже эталонного, но тяготение параметров золотин к одной прямой позволяет относить их к одной группе
Таблица 1. Параметры зерен золотин в россыпях Якутии и Тимана [11]
|
№№ пп.
|
№№ пробы
|
Вес в мг
|
Размеры по осям (мм)
|
V= АВС
мм3
|
|
А
|
В
|
С
|
|
1
|
3
|
0,07
|
1,2
|
0,66
|
0,005
|
0,039
|
|
2
|
6
|
0,12
|
1,1
|
0,62
|
0,01
|
0,007
|
|
3
|
6а
|
0,25
|
0,26
|
0,24
|
0,2
|
0,013
|
|
4
|
10
|
0,46
|
1,23
|
0,69
|
0,03
|
0,025
|
|
5
|
11
|
1,12
|
4,51
|
2,73
|
0,005
|
0,062
|
|
6
|
12
|
4,02
|
4,51
|
2,45
|
0,02
|
0,221
|
|
7
|
17
|
2,68
|
3,50
|
2,11
|
0,02
|
0,148
|
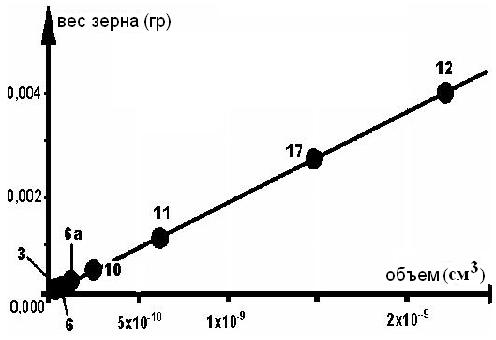 Рис. 1. Характер зависимости размерных и весовых параметров золотин. Числа у точек- номера проб согласно таб. 1
Рис. 1. Характер зависимости размерных и весовых параметров золотин. Числа у точек- номера проб согласно таб. 1
Таблица 2. Соотношения между весом и размерными параметрами
россыпного золота
|
№№
п.п.
|
№№ выборки
|
Место отбора пробы
|
P = ρV + A
|
|
ρ
|
A
|
R2
|
|
01
|
SUR-02-1
|
р.Б. Рудневка, аллювий
|
6,281
|
-0,0071
|
0,994
|
|
02
|
SUR-02-2
|
р.Б. Рудневка, аллювий
|
11,74
|
-0,0617
|
0,906
|
|
03
|
SUR-03.
|
Приморье, Бухта Руднева,
|
4,523
|
-0,0003
|
0,986
|
|
04
|
SUR-05
|
бух.Тепа-2, Тугурский зал.,
Охотское м.
|
9,166
|
-0,029
|
0,995
|
|
05
|
SUR-07.
|
Бухта Магма, пляж
|
2,694
|
0,0661
|
0,945
|
|
06
|
SUR-08
|
Зап.Камчатка, Митога, пляж
|
13,30
|
-0,0231
|
0,928
|
|
07
|
SUR-06
|
Бухта Тепа-2, древний аллювий
|
11,45
|
0,0351
|
0,981
|
|
08
|
SUR-10
|
Забайкалье, росс. Гулинга,
аллювий
|
9,31
|
0,0896
|
0,991
|
|
09
|
SUR-04
|
Бухта Тихангоу
|
10,78
|
-0,029
|
1,000
|
|
10
|
SUR-09.
|
Кулар, росс. Кыылах,аллювий,
плотик
|
11,62
|
-0,0315
|
0,981
|
типоморфных зерен. По величине ρ золотины находятся в промежутке между призмоидной и эллипсоидной группами [2]. Наблюдаются и более существенные отклонения; они приведены в [3].
2. В ряде случаев удается выделить несколько групп типоморфных зерен; например, в аллювии реки Б. Рудневка выявлены две такие группы. Иногда [6, 9] появление таких групп трактуется как результат поступления золота из других источников, хотя возможно, что это - результат проявления изменения гидродинамических условий транспортировки золотин.
3. Гипотетически уравнения распределения параметров золотин должны иметь вид P = ρV. Фактический материал не подтверждает предположение: все уравнения имеют вид P = ρV + A. Смысл параметра A пока не ясен. Его можно трактовать как ошибку в построении прямых.
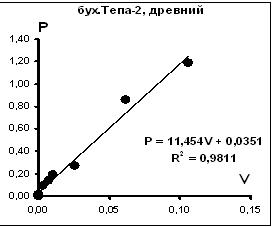
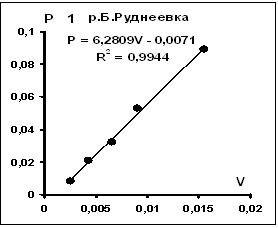
Рис.2. Связь между весом P и объемом V Рис.3 Связь между весом P и объемом V
золотин из россыпи бух. Тепа-2. золотин из аллювия р. Б.Рудневка.
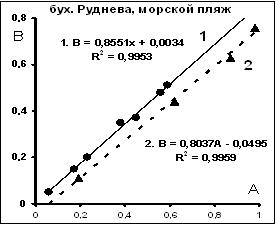
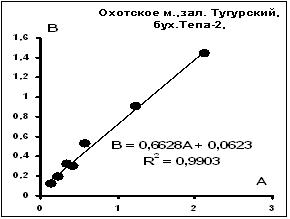
Рис. 5. Распределения параметров А и В Рис. 6. Распределения параметров А и В
золотин из отложений морского пляжа. золотин из отложений речного аллювия
Б. Соотношения между размерными параметрами золотин.
1.Распределение параметров А и В. Это основная форма изучения поведения золотин в потоках. Этим измерениям подвергнут широкий круг объектов, сюда вошли не только данные по россыпям, но и результаты опробования продуктов дражного обогащения. Особенности измерений этих параметров отражены в работе [6, 9]. Наиболее низкая точность измерений характерна для оси С.
Таблица 3. Основные параметры распределений параметров А и В золотин. Уравнение В= nА + N
|
№№
п.п.
|
№№ вы-борки
|
Место отбора пробы
|
n
|
N
|
R2
|
|
01
|
SUR-03-2
|
бух.Руднева, морской пляж
|
0,8037
|
-0,0495
|
0,996
|
|
02
|
SUR-05
|
бух.Тепа-2, Тугурский зал., Охотское м.,
|
0,6628
|
0,0623
|
0,99
|
|
03
|
SUR-07.
|
бух.Магма, пляж
|
0,7664
|
-0,0092
|
0,925
|
|
04
|
SUR-09-2
|
Кулар, рос. Кыылах, аллювий, плотик
|
0,511
|
0,2251
|
1,000
|
|
05
|
SUR-10
|
Ципиан, рос.Гулинга, аллювий
|
0,5737
|
0,1519
|
0,936
|
|
06
|
SUR-12
|
Прииск Заамар, уч. Северный, эфеля
|
0,8038
|
-0,0233
|
0,985
|
|
07
|
SUR-13
|
Прииск Заамар, уч. Южный, эфеля
|
0,7671
|
-0,0195
|
0,986
|
|
08
|
SUR-11-2
|
прииск Толгойт, эфеля, хвосты
|
0,9602
|
-0,1489
|
0,988
|
|
09
|
SUR-04.
|
бух.Тихангоу, эфеля аллювия
|
0,751
|
-0,0488
|
0,962
|
|
10
|
SUR-02.
|
р.Б. Рудневка, аллювий
|
0,5328
|
0, 0707
|
0,945
|
|
11
|
SUR-06
|
бух.Тепа-2, древний аллювий
|
0,5279
|
0,0646
|
0,988
|
|
12
|
SUR-11-1
|
Монголия, прииск Толгойт
|
0,5851
|
0,0101
|
0,992
|
|
13
|
SUR-08
|
Зап.Камчатка, район Митоги, пляж
|
0,3537
|
0,1769
|
0,900
|
|
14
|
SUR-09-1
|
Кулар, рос. Кыылах, аллювий, плотик
|
0,5674
|
0,0037
|
1,000
|
|
15
|
SUR-11-3
|
прииск Толгойт, эфеля, хвосты
|
0,9098
|
-0,7933
|
1,000
|
|
16
|
SUR-03-1
|
бух.Руднева, морской пляж
|
0,8551
|
0,0034
|
0,995
|
|
Пояснения: бух.- бухта; зал.- залив; м.- море; рос.- россыпь; уч.- участок;
|
Основной метод изучения - построение диаграмм в координатах (А,В). Примеры этих построений приведены на рис. 5, 6. На рис. 7 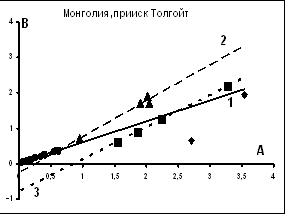 Рис.7. Распределения параметров А и В золотин из продуктов дражной промывки на прииске Толгой
Рис.7. Распределения параметров А и В золотин из продуктов дражной промывки на прииске Толгой
приведены данные по отходам дражной промывки (эфеля лежалые и текущие, хвосты ШОУ, торфа) прииска Толгойт (Монголия). Аналогичные образования изучены и на приисках Заамар Северный и Заамар Южный (Монголия). Основные результаты построений отражены в табл. 3 в виде параметров уравнений В= nА + N . Во многих россыпях выявляется по несколько генераций золотин. В табл. 3 они отмечены для бухты Руднева, Кыылах (С.Якутия), прииска Толгойт. На рис.5, 7 приведены примеры подобных распределений. На рис.7 номера выборок (прямых линий) соответствуют их порядку в табл. 3.
Рис. 8. Сводная диаграмма поведения параметров А и В золотин.
На рис. 8 и 9 приведены сводные диаграммы распределения параметров А и В, учитывающие распределение золотин объектов нескольких регионов. На
рис.8 для золотин с параметрами А ≤ 1 мм и В ≤ 1 мм прямая В= nА + N
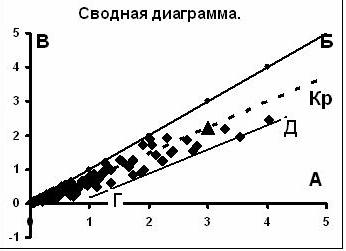
Рис.9. Сводная диаграмма поведения параметров А и В золотин для широкого круга объектов.
описывает использованные объекты и имеет очень небольшую поперечную дисперсию. Однако для более широкого круга объектов эта закономерность нарушается. Это видно на рис.9, построенном по данным всех объектов, имеющихся в нашем распоряжении. Здесь прямая ОБ- биссектриса, она отражает условие А = В, характеризующие равновесие в формировании золотин. Рис.9 показывает, что несмотря на высокую устойчивость соотношений параметров А и В, последние не являются равновесными. Согласно рис.9 при А > 1 мм и В > 1 эта дисперсия существенно увеличивается, сохраняя, однако, общую согласованность поведения параметров А и В.
Гипотетически зависимость между параметрами должна иметь вид В = nА. Действительно, если размер золотины по одной из осей равен нулю, то это означает, что нет и самой золотины. Фактическое распределение параметров А и В в конкретных выборках описывается уравнением прямой линии В= nА + N, причём величина Nсоизмерима со значениями величин А и В. Механизм формирования такой зависимости не ясен.
2. Распределение параметров А и С.
Здесь проблема анализа этого распределения оказалась более сложной в связи с низкой точностью замеров по оси С, тем не менее и здесь получены определенные результаты. В целом толщина золотин (размер по оси С) низкая, как правило закономерных комбинаций с величиной А она Таблица 4. Основные параметры распределений параметров A и С золотин.
|
№№ выборки
|
Место отбора проб
|
Виды уравнений
|
R2
|
|
SUR-03-2.
|
бух.Руднева,морской пляж
|
C2 = -0,0484A + 0,0597
|
0,987
|
|
(1/C2) = 73,228A + 7,874
|
0,997
|
|
SUR-04.
|
бух.Тихангоу, эфеля
|
C1 = -0,0937A + 0,0887
|
0,890
|
|
C2= -0,0362A + 0,1365
|
0,962
|
|
SUR-07-1.
|
бух.Магма, пляж
|
C1 = -0,2684A + 0,3383
|
0,929
|
|
SUR-07-2
|
C2 = -0,5821A + 0,367
|
0,964
|
|
|
(1/C2) = 53,094A - 13,569
|
0,995
|
не несет, хотя в ряде случае выявляется линейная связь с длиной золотины. Такие результаты отражены в таб.4. На рис. 10 приведены примеры распределений. Во всех случаях выявляется распределение, обратное распределению величин по оси А, которое часто переходит в гиперболическую зависимость (рис. 11); здесь нет противоречия: часть гиперболической кривой на значительном числовом интервале может апроксимироваться прямой линиейнойз ависимостью. В установленных
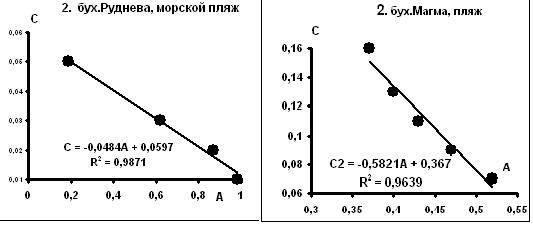
Рис. 10.Распределение параметров А и С в россыпях бухт Магма и Руднева.
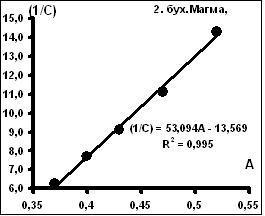 Рис. 11. Пример гиперболического
Рис. 11. Пример гиперболического
распределения.
случаях размеры золотин по оси С изменяется обратно пропорционально таковым по оси А.Известно, что золото обладает кубической сингонией и для него, как правило, характерны октаэдрические кристаллы. Пример такого кристалла приведен на рис.12. В целом, октаэдрическая форма для золота – не частое явление. Тем не менее, именно она помогает понять
Рис. 12.Октаэдрический Рис. 13. Варианты расположения сил при
кристалл золота. Сысертекий ударном воздействии на кристалл
район (Урал) [1].
выявленные особенности морфологии золотин в россыпях, если положить, что на морфологию золотин существенно влияют ударные воздействия. Последних может быть два вида:
1. в процессе переноса потоком зерно ударяется о некоторую твердую поверхность (гальку, валун и пр.);
2. в процессе переноса золотина находится под ударным воздействием двух галек, между которыми золотина попадает.
Наиболее эффективный результат будет получен, если сила удара пройдет через центр тяжести. В противном случае возникнет вращающий момент, который ослабит силу удара. Здесь также возможны варианты распределения сил:
1. направление удара (сжатия) проходит через две противоположные вершины;
2. направление удара (сжатия) пройдет через два противоположных ребра. Эффекты от этих вариантов удара различны.
Второй вариант расположения сил наиболее вероятен, схема возможных эффектов приведена на рис. 13. На этом рисунке Р- сжимающее усилие, dL- изменение размеров золотин по осям А и В соответственно.
Поскольку золото обладает кубической сингонией, то размеры кристалла по направлениям АА, ав и бг равны, т.е. АА = ав = бг. При действии сжимающего усилия размер кристалла аг и бв будет уменьшаться, формируя ось С, а в направлениях АА и ВВ - увеличиваться. Действительно, пусть исходный объем кристалла равен Vo= AoBoCo, после воздействия сжимающего усилия он станет Vр= AрBрCр. Если Vo= Vp, то AoBoCo= AрBрCр и (Ао/Ар)(Во/Вр)(Со/Ср) = 1. Отсюда уменьшение одного сомножителя приведет к росту величины второго сомножителя. По экспериментальным данным A= nB, поэтому nA2C=1, а значит рост
параметра А приведет к уменьшению параметра С. Из рис.12 ясно, что изначально всегда А > B; действительно, в квадрате абвг диагональ ав (гипотенуза равнобедренного прямоугольного треугольника авг) соответствует размеру по оси А, а ось ВВ - катету этого равнобедренного прямоугольного треугольника. Следовательно при данном действии сил изначально будет формироваться призма с разными размерами по соответствующим осям, причем всегда А ≈ ВÖ2, т.е. В/А ≈ 0,707 (Ö - корень квадратный). В то же время при действии сил в направлении вершин А-А будет формироваться плоская призма (табличка), в которой А ≈ В. Проведенные построения позволяют предположить, что отношение осей В/А ≈ 0,707 будет исходным. С целью проверки этого предположения на диаграмму рис.9 вынесена прямая О-Кр, угловой коэффициент которой равен 0,707. Сопоставление показывает, что, несмотря на различные частные отклонения в конкретных условиях, в общем случае подавляющее количество точек, для которых А ≤ 1,5 мм, точно ложится на прямую О-Кр. При более крупных размерах золотин дисперсия распределения точек увеличивается, но это исходное отношение, отражаемое прямой Г-Д, сохраняется. В то же время на биссектрису О-Б, соответствующей равенству А = В и первому механизму действия сил, попадает крайне ограниченное количество золотин.
ОСНОВНЫЕ ВЫВОДЫ
Проведенные исследования показали, что в песчано-алевритовой фракции россыпей золотины слагают неполные регулярные множества типоморфных зерен, в них практически постоянным является отношение размеров осей В/А, распределение размеров золотин по оси С подчиняется гиперболическому закону. Основная форма золотин - призмоидная (почти прямая призма). Установлено, что отношение В/А по величине близко отношению осей кристалла золота - октаэдра.
Таким образом, в россыпях поведение золота отличается от поведения других минералов, например, кварца. Кварц ведет себя как хрупкое вещество. В то же время золотины - это кристаллы, пластически деформированные, но сохранившие соотношения основных параметров решётки.
Литература.
1. Бетехтин А.Г. Минералогия. М.: Госгеолиздат, 1950. 956 с. с ил.
2. Макаров В.П.К определению понятия «обломочные породы». Мат-лы 4- го Всерос. совещ. «Осадочные процессы: седиментогенез, литогенез, рудогенез (эволюция, типизация, диагностика, моделирование). М.: ГЕОС, 2006. Т.1. С.119 - 122.
3. В.П. Макаров. Некоторые вопросы теоретической геологии. 5. О форме зёрен в аллювиальных отложениях./ Материалы конференции «Научные исследования и их практическое применение. Современное состояние и пути развития ‘2007». Одесса: Черноморье, 2007. С 27-38.
4. Рухин Л.Б. Гранулометрический метод изучения песков. Л.: Изд-во ЛГУ, 1947. 213 с.
5. Рухина Е.В. Литология ледниковых отложений. Л.: Наука,1973. 176 с.
6. Самыкина Е.В., Сурков А.В. Самородное золото и алмазы. Особенности их плотности и формы как основных технолог. характеристик при геологоразведочных работах и освоении россыпных месторождений. /XI научный семинар «Система планета Земля». М. Изд. МГУ, 2003. С.146- 151.
7. Сочнева Э.Г., Прокопчук Б.И. Минералогический анализ тяжелой фракции терригенных отложений. М.: Недра, 1976. 143 с.
8. Сурков А.В. Методика грануло–минералогического анализа при изучении обломочный пород. // Изв. ВУЗ–ов. Геология и разведка, 1993. №3. С. 36
9. Сурков А.В. Атлас форм самородного золота (золотин).М.: изд.«СтудиА», 2000.Т.1.70с.
10. Сурков А.В. Новое в изучении песчано-алевритовой компоненты россыпей и осадочных пород. М.: издатель Е Разумова, 2000. 286 с.
11. Сурков А.В., Фортунатова Н.К., Макаров В.П. Об условиях образования современных осадков Чудского озера по гранулометрическим данным.// Изв. вузов. Геология и разведка, 2005. 5. С. 60 – 65.
Примечание: Источник - Макаров В.П., Сурков А.В. Вопросы теоретической геологии. 6. О форме золотин в россыпях. //Международная научно-практическая конференция «Нау-чные исследования и их практическое применение. Современное состояние и пути развития ‘2007». 1-15 окт. 2007. Одесса: Черноморье, 2007, Т.16. С. 38 47.
Рис. 1. Характер зависимости размерных и весовых параметров золотин. Числа у точек- номера проб согласно таб. 1
Рис.7. Распределения параметров А и В золотин из продуктов дражной промывки на прииске Толгой
Комментарии
You may like my work
Dear Mr. Makarov,
I can read Russian, but my PC is not adjusted for azbuka, so I prefer writing you English. I am impressed by your publications.
You may like my theroretical and practical results in Sand Texture Sedimentology. You are welcome on my web pages:
http://www.grano.de
My email: jb@grano.de
Best wishes,
Jiri