«Явление компенсации» - новый вид связи между геологическими объектами.
«Явление компенсации» - новый вид связи между геологическими объектами.
Макаров В.П.
Российский государственный геологоразведочный университет. Москва.
При обработке первичной информации о вещественном составе объектов часто применяют функциональные зависимости. В связи с простотой в вещественных полях ( гео-, петрохимических и пр.) широко используются линейные или линеаризованные (например, уравнения регрессии) зависимости между параметрами вида Y= АХ+ В (X и Y- значения параметров: содержание, концентрация, плотность и пр.; А и В- постоянные). Как пример ниже приведен ряд зависимостей:
1. Линейные зависимости:
1а. 206С = а6204С + А6 [3];
1б. S298o = a + b(Cp298o) (М.Х. Капустинский)
2. Линеаризованные зависимости:
2а. 206С = b6/Pb + B6 [3];
2б. ln(K/Ko) = -A/T +B;
2в. 1000lna(M-C) = A/T2 – B [Bigeleisen J., 1961];
2г. D = Do exp(-Е/RT) и т.д.
Линеаризация осуществляется преобразованием Х= 1/Р (1/Р2), где Р- переменный параметр, или логарифмированием параметров соответствующих уравнений, могут быть и другие формы. Часто физический смысл параметров, входящих в них, не известен, например, в уравнениях (1б), (2б - 2г). Тем не менее, при наличии нескольких выборок вида Y= АiX + Вi между ними возможна связь в виде "уравнения компенсации" В= -XoА+ Yo, где (Xo,Yo)- координаты точки пересечения пучка частных прямых [5].
В отечественной литературе представления о «компенсации» используются в связи с анализом диффузионных процессов. Оттуда же заимствована и терминология. Сущность явления «компенсации» изучена не достаточно. Некоторые аспекты компенсации рассмотрены В.М. Катлинским [4]. Анализ явления выявил возможность использования «компенсации» в решении геологических задач. В геологической литературе попытки использования ее предпринимал, хотя и не совсем удачно, Н.Д. Сорокин [41]. Проблемы диффузии и компенсации изучены нами [13, 16, 18, 25, 28, 29, 37]. Перед анализом «компенсации» оценим распространенность явления в природе.
А. Влияние диффузии на процессы формирования геологических объектов известно давно. Представления о диффузии применяются в нефтегазовой геологии и гидрогеологии для анализа условий существования нефтяных и газовых залежей [Дж. Хант,1982]. Менее широко они применяются в геохронологии с целью изучения процессов миграции радиогенных изотопов.
При анализе рудных и силикатных систем использование представлений о диффузии носило характер гипотетических суждений. Основной объем работ в этой области включал эксперименты по определению параметров диффузии в расплавах либо твердых телах при различных температурах Т и давлениях P без четкого понимания, для чего они нужны. Для корректировки изотопных геотермометров определены диффузионные параметры некоторых изотопов легких элементов без разработки методики их использования.
В настоящее время имеется большое количество определений параметров диффузии, обладающих, однако, существенным недостатком: слабой сходимостью для одних и тех же условий параметров, определенных разными авторами. Имеется не менее 14 уравнений диффузии кислорода в полевых шпатах при примерно равных температурных интервалах; кислорода в a-Ti - 9; Na в альбит – 10, калия там же – 4 и т.д. Это же относится и к определениям коэффициентов диффузии изотопных компонентов в минералах, например, изотопов O и C в кальцитах. Эти расхождения неоднократно обсуждались в литературе, например, [2], однако до сих пор проблема не решена. 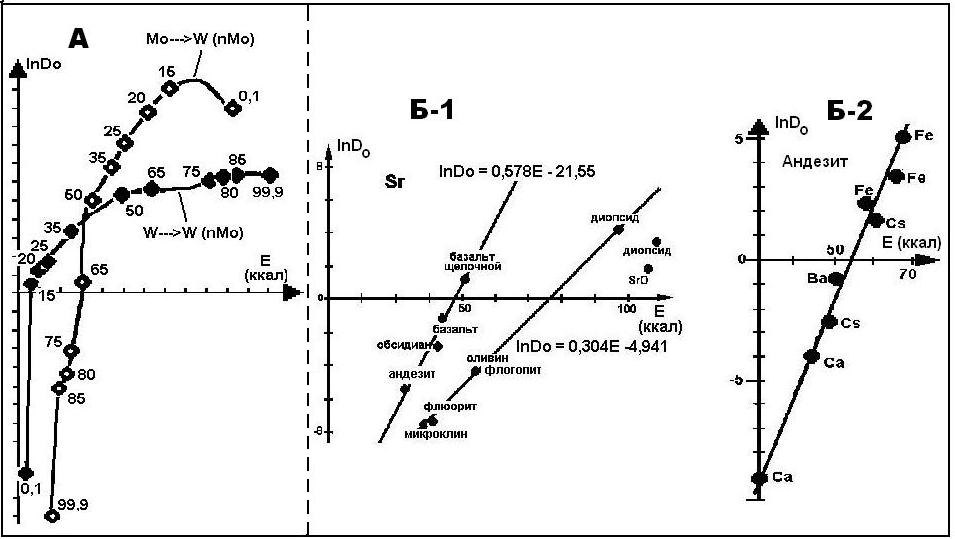
Рис. 1. Распределение параметров диффузии в сплавах Mo и W и породам по данным различных авторов. А- в сплавах Mo и W; Б-1 и Б-2 – породах.
Уравнения диффузии обобщаются через компенсационные уравнения (далее КУ) lnDo=aЕ +А, в которых переменными уже являются параметры Doи Е. Проведенные исследования с использованием базы данных по значениям Е и Do, включавшей минералы (Т=200-800оС), расплавы пород (Т= 900-1440оС), более простые системы (искусственные стекла, сплавы) с переменным составом-(Y2O)(Y2O)4(SiO2), (Y2O)3(SiO2) (Y=K, Na, Li, Cs); (Y2O)(XO)4 (SiO2) (X=Ca, Mg, Sr, Ba), показали отсутствие широких возможностей в построении компенсационных уравнений. Так нами построено 49 компенсационных прямых, охватывающих всего 30% объема базы данных. Подавляющее большинство сплавов либо не имеет, либо имеет нечетко выраженные КУ, либо связь Е c Doимеет более сложный характер. Примеры этих распределений приведены на рис.1А, построенном по данным изучения сплавов Mo с примесью W и W с примесью Mo; он показывает, что диффузионные параметры не описываются общей компенсационной прямой.
На рис. 1Б показаны распределения параметров диффузии в более сложных системах. Четко проявляется компенсация, она выполняется в стеклах, сложных природных системах: минералах (альбит, ортоклаз и др.), породах (обсидиан, фонолит, андезит, базальт) [13, 16, 18]. Среди них выявлены два основных типа, не выделяемых Н.Д. Сорокиным [41].
1.(КУ-1) Распределение одного и того же диффунданта в матрицах разного состава (рис.1Б-1). В простейших системах положение прямых КУ определяется, в первую очередь, валентностью диффунданта. Так в стеклах если дан У+1, то прямые КУ совпадают. Для ионов У+2 прямые КУ уже разделяются. Как видно из рис. 2А для одного и того же элемента (Sr) в разных исходных базах (породы и минералы) КУ оказываются различными.
2. (КУ-2) Распределение диффундантов в одной и той же матрице (рис. 1Б-2). Положение компенсационных прямых зависит от состава матрицы. В искусственных стеклах, если Y= Na, то по величине Е катионы образуют последовательность: Na< Li< K< Rb< Cs; Y= K: K< Rb< Na< Cs; Y= Cs: Cs< Rb< Na; Y= Rb: Rb< K< Cs< Na. Минимальной энергией Е обладают элементы самой матрицы. Для матриц с двухвалентными диффундантами на первом месте стоит диффундант, сумма ионного радиуса которого с радиусом элемента матрицы обладает минимальными значениями, приближаясь к величинам расстояний между элементами матрицы и ионом кислорода. Прочие диффунданты следуют по возрастанию атомного веса или ионного радиуса. Существующие попытки интерпретации касаются только КУ-1 (теория Верта-Зинера - Ле Клера [2, 6, 39] и др.).
Описание уравнений компенсации базируется на представлении уравнения диффузии в качестве уравнения прямой, проходящей через заданную эталонную точку. Если эта точка –общая для диффундантов, то образуется компенсационное уравнение lnDo= Е/RT*+ lnD* с параметрами (точки кроссовера) T* и lnD*. Здесь выявляется вторая ошибка Н.Д. Сорокина, который связывал положение компенсационной прямой с механизмом диффузии. При интерпретации уравнений компенсации Н.Д. Сорокин опирался на эмпирическое равенство Динеса (1950 г.) [6, 41].
Нами установлено, что для расплавов T* > Tпл (Тпл – Т плавления матрицы), для твердых тел (кристаллов) T*< Tпл, приближаясь к Т их образования [13, 16, 18, 28] в природных условиях (например, для альбита Т* = 421оС (Тобр= 500оС [13, 34]), калишпата– 507 (Тобр = 550оС), флогопита – 483 (для биотита Тобр = 650оС), сфалерита – 624оС). Использование равенства D*=knd(n–частота колебания диффундирующего атома около положения равновесия, d–постоянная решетки (межатомное расстояние(?)), k= const) не перспективно, поскольку компенсационные прямые объединяют матрицы с переменными значениями n и d.
Б. В работе [38] рассмотрены некоторые свойства «геохимических геотермометров», описываемых уравнением lnKp= -A/T+ B, где Kp– коэффициент распределения концентраций элементов между двум фазами; Т(оК)- температура, А и В – постоянные. Поскольку они 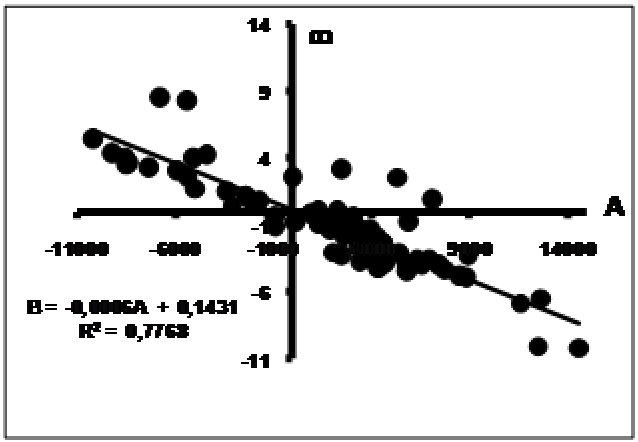
Рис.2. Компенсационная диаграмма параметров уравнений геохимических геотермометров.
имеют линейный характер, то к ним применены представления о «компенсации». По имеющимся данным построена компенсационная диаграмма (рис.2). Если удалить точки, существенно отскакиваемые от результативной прямой и потому оцениваемые как ошибочные, то окончательное уравнение имеет вид В = -0,0005А - 0,3424. Таким образом в среднем имеет место равенство А/В ≈ 2000.
В. В работе [40] рассмотрены результаты изучения минерального состава мраморов и кальцифиров Украины. Графики относительных содержаний главных минералов выявляют линейную зависимость между этими количествами, описываемую уравнением у = Ах + В; (у – концентрации кальцита, х– доломита). На рис.3 показана графическая связь между этими параметрами и приведено компенсационное уравнение. На рис.3 Фл–флогопитовый, Фр –форстеритовый, Шп–шпинелевый мрамора. Рисунок демонстрирует выполнимость явления компенсации применительно к количественным параметрам распределения минералов в породах и слабую зависимость этого явления от состава породы.
Рис.3.Вид компенсаци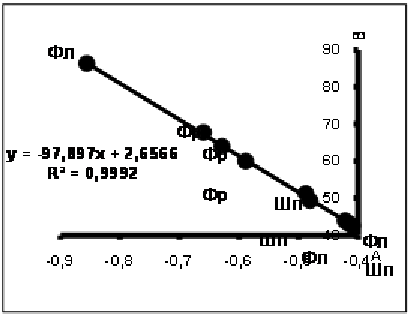 онной прямой.
онной прямой.
Г. В работе [1] описаны результаты оценки скоростных параметров разреза по данным промыслово-геофизических исследований на Салымской площади. Определялись скорость Vp (км/с) упругих волн в породах, кажущееся удельное электрическое сопротивление (по каротажу) rk и гамма излучение Jk. В процессе исследований выявилось наличие функциональной зависимости между этими параметрами вида Vp = А(lgrk) + В. Анализ показывает наличие явления компенсации между геофизическими параметрами Vp и lgPk. Явление компенсации между Vp и lgJk отражается уравнением Vp = -0,1909 lgJk + 0,6312 .
Д.В практике исследований нефти широко использовались измерения её плотности d, показателя преломления n и кинетической вязкости ν, связь между первыми, как известно, имеет вид nD20= Ad420+ B, где d420 – плотность нефти, измеренная при 20оС и отнесённая к плотности воды при 4оС, nD20- показатель преломления нефти, измеренный для линии D натрия при температуре 20оС.
При использовании представлений о компенсационных уравнениях установлено, что в координатах (А, В) все точки легли на единую прямую линию [45]. На её основе проведена оценка физических параметров no и do нефти в её источнике с помощью теории решения задачи об источниках вещества [37, 44], которая и оперирует с параметрами А и В. Этим уравнениям соответствует пара чисел (А, В). Тогда, используя их как некоторые координаты для нескольких прямых, можно построить прямую вида B= аA+ в [37, 44]. Уравнение вида B= (-Aо)A+ Bо и есть компенсационное уравнение. 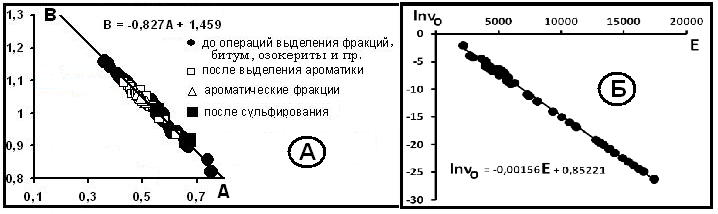
Рис. 4. Компенсационная диаграмма для нефти: А -по параметрам уравнения n=Ad + B; Б – для параметров вязкости lnν = lnνo + E/RT
Во многих работах приведены значения кинетической вязкости при температурах 20 и 50оС (293 и 323оК). В литературе упоминаются основные уравнения, связывающие кинетическую ν (или динамическую μ) вязкость с температурой. Для их оценки рассчитаны уравнения, связывающие параметры d и n в уравнение (1). Получены 103 выборки анализов, по которым построена компенсационная диаграмма (рис.4-А). Чётко выявляется принадлежность всех точек углеводородов только к прямой линии с уравнением B= -0,827A+ 1,459; тогда координаты точки кроссовера имеют значения: do= 0,827 и no= 1,459. lnν= lnνo+ E/RT. Здесь Т - температура в оК; Е – энергия активации вязкого течения. Большое количество объектов позволяют использовать принцип компенсации для параметров Е и lnνo. Диаграмма компенсации приведена на рис. 4-Б, точки всех месторождений ложатся на одну прямую. В источнике преобладала T= 40 – 50оС и lnνо= 0,8522 (νо ≈ 2,34 сСт).
Рис.А. Компенсационые прямые для россыпного золота.
Е. Россыпное золото (золотины) в широком географическом интервале детально изучалось А.В. Сурковым [46]. Исследования заключались в измерениях размеров золотин по осям A, B и C по методике, описанной в [47]. В результате обработки этих данных [48, 49] установлено наличие связи вида B=mА + M. В этот же набор исследований входило и построение компенсационных прямых. Рузультаты этих работ отражены на рис.А. Выявлены два семейства золотин с параметрами, приведёнными на рис.А, но природа их не ясна.
Ж. Романовский С.И. [50], анализируя зависимость мощности слоев от размеров выволняющего слой зерна, опирается на выражение
d = АMа,
где d - размер частиц (в данном случае максимальный), M - мощность слоя, a и А - постоянные, физический смысл которых не установлен. Преобразовав это уравнение в уравнение вида
log d = logА + а logM,
по литературным данным он собрал соответствующие практические уравнения в таблицу, по данным которой построена компенсационная диаграмма на рис. Б. Как видно эти литологические параметры хорошо описываются уравнением компенсации с параметрами, приведёнными на .
|
Фактический материал |
Уравнение регрессии |
Коэффициент корреляции ρ |
Первоис- точник |
|
Морские песчаники Французских Альп (палеоген-неогенового возраста) |
lgdmax = -1,74 +0,69lgξ* |
0,78 |
Potter P.E., Scheidegger C. 1966 |
|
Мартинбургская формация в Пенсильвании (ордо-вик) |
lgdmax = -0,81 + 0,36lgξ* |
0,84 |
|
|
Нумулитовый флиш |
lgdmax = -1,17 + 0,44 lgξ* |
0,73 |
|
|
Смесь данных |
lgdmax = -1,18 + 0,57lgξ* |
0,72 |
|
|
Пепел вулкана Гекла |
lgdmax = -0,53 + 0,92lgξ* |
0,99 |
|
|
Терригенный флиш |
lgξ* = 2,37 + 1,28 lgdcp |
- |
Рац М.В. 1962 |
Рис.Б. Компенсационная диаграмма по литологическим данным.
рис.Б. Отдельно от все массы осадков стоит пепел вулкана Гекла , говоря. видимо, о другой его природе.
Е.И3ОТОПНЫЕ СИСТЕМЫ
Собран и обработан большой литературный материал по распределениям в минералах как самих элементов, так и их изотопов. Этот материал касается изотопов Pb, Ne и стабильных изотопов легких элементов δD, δ18O, δ13C, δ34S. Ниже эти системы мы опишем раздельно.
I.Карбонатные образования. Изучены кальциты гидротермальные, скарнов, мраморов, кальцифиров, кимберлитов, карбонатитов, конкреций, сталактитов и биогенных, различных видов современных и древних организмов [12, 17, 21–24, 30]. Фактический материал позволил построить компенсационные зависимости для этих кальцитов (табл.1). Результаты приведены на рис. 5–9 по генетическим типам кальцитов.
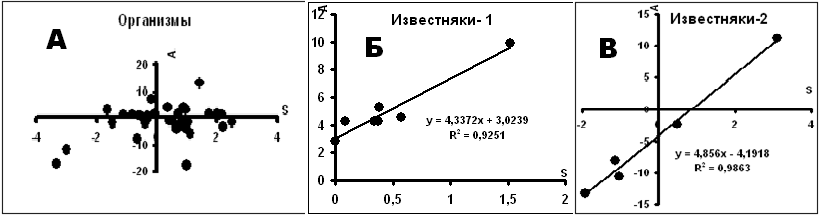
Рис.5. Распределение параметров уравнений вида δ13C= Sδ18O+ A в экзогенных образованиях. А - в органогенных кальцитах: Б и В – в различных известняках.
Таблица 1. Сводные данные по значениям исходных параметров.
|
№ п.п. |
Семейство |
Выборка |
Кол-во |
Параметры ур-ния компенсации |
R2 |
|
|
g |
G |
|||||
|
1 |
I |
Карбонатит |
28 |
20,846 |
-4,5299 |
0,9854 |
|
2 |
Кимберлит |
12 |
14,443 |
-3,7678 |
0,9317 |
|
|
3 |
Скарны |
8 |
-12,761 |
-2,1738 |
0,9676 |
|
|
4 |
Гидротерм-1 |
29 |
23,947 |
-4,4244 |
0,918 |
|
|
5 |
Известняк-2 |
5 |
7,856 |
-4,1918 |
0,8863 |
|
|
6 |
II |
Мрамор-2 |
7 |
20,591 |
-7,3352 |
0,9381 |
|
7 |
Травертин |
3 |
36,267 |
-3,3941 |
0,9717 |
|
|
8 |
Сталактит |
3 |
4,6401 |
-12,126 |
0,9763 |
|
|
9 |
Диагенетич. |
6 |
7,0383 |
-11,476 |
0,7789 |
|
|
10 |
|
Мрамор-1 |
13 |
-12,936 |
1,0402 |
0,9922 |
|
11 |
|
Гидротерм-2 |
4 |
7,1277 |
-0,2723 |
0,9606 |
|
12 |
|
Известняк-1 |
7 |
4,3372 |
3,0239 |
0,9251 |
А). Биогенные кальциты (и арагониты) [21 –24]. Как видно из рис.5, в этих кальцитах трудно говорить о проявлении компенсации.
Б). Экзогенные (низкотемпературные) кальциты [21–24, 30]. В эту группу включены кальциты диагенетические, сталактиты, травертины, известняки. Есть мнение, что в образовании этих кальцитов существенную роль играли микроорганизмы. Компенсационные диаграммы приведены на рис. 6. Параметры исходных составов показаны на рисунках в виде параметров уравнений компенсации.
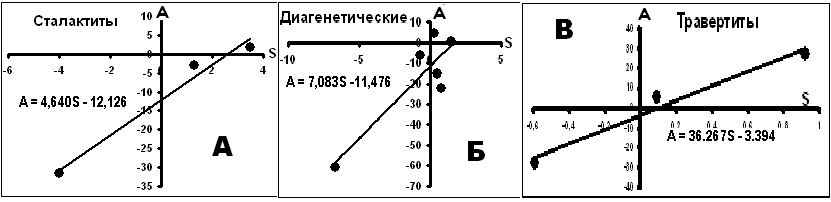
Рис.6. Распределение параметров уравнений вида δ13C = Sδ18O + A в экзогенных кальцитах.
В). Кальциты гидротермальные [24]. Диаграммы представлены на рис.7. Исходные параметры приведены на графиках в виде параметров уравнений компенсации. 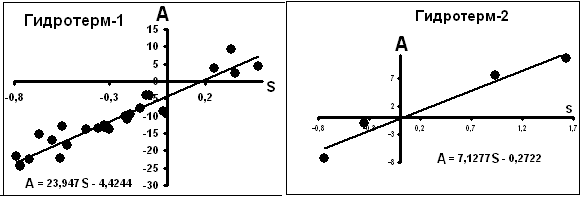
Рис.7. Распределение параметров уравнений вида δ13C= Sδ18O+ A в гидротермальных кальцитах.
Г). Высокотемпературные кальциты [12, 17, 21, 24 ]. Это - кальциты мраморов, скарнов, кальцифиров, кимберлитов. На рис.8 приведены данные для мраморов и скарнов. Выделяются две группы мраморов с различными значениями исходных параметров (параметры уравнений компенсации). На рис. 9–данные для кимберлитов и карбонатитов.
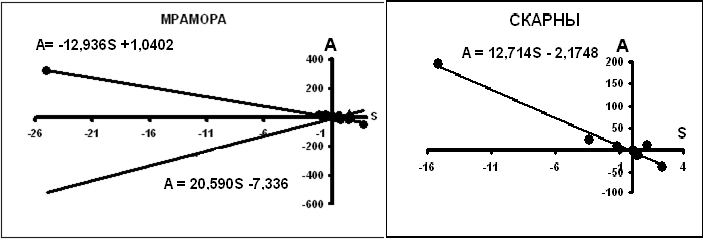
Рис.8. Распределение параметров уравнений вида δ13C = Sδ18O + A в кальцитах мраморов и скарнов.
Д). Магматические кальциты [24]. Распределение параметров изотопных уравнений приведено на рис.9, иллюстрирующий наличие компенсации. Таким образом, практически во всех кальцитах неорганического происхождения наблюдается явление компенсации, причем с ростом Тобр минерала возрастает четкость ее проявления.
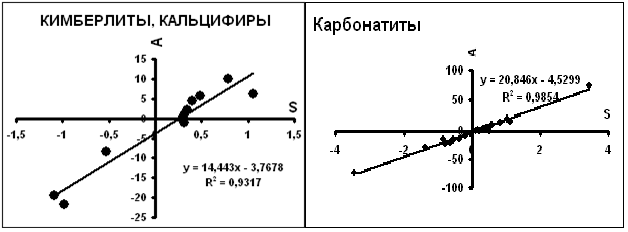
Рис.9. Компенсационные диаграммы для кимберлитов и карбонатитов.
В целом уравнения компенсации имеют вид В= gА + G, где g и G- параметры уравнения. По этим данным выделяются два множества объектов:
:а) группа с наибольшим количеством выборок, в которых g> 0;
:б) группа с меньшим количеством членов g< 0. Во второе множество входят кальциты скарнов и мраморов, которые изначально развиваются по органогенным породам (известнякам). В этом множестве направление прямых совпадает с тенденцией поведения параметров изотопных уравнений в органогенных кальцитах.
II. Сульфидные образования. Изучено распределение изотопов серы в виде показателя δ34S в галенитах, сфалеритах, халькопиритах, пиритах, пирротинах различных месторождений мира. При работе выявился ее существенный недостаток - нехватка фактического материала, из-за этого появились проблемы в составлении однородных выборок. Дело в том, что сульфиды представлены большим количеством минеральных видов, слагающих рудные тела разных типов (залежи, стратиформные (СФ) и вкрапленных рудные тела и жилы (ЖЛ)) в широком круге промышленных типов месторождений в различных регионах мира. Практически конкретное месторождение обладает очень малым количеством изотопных уравнений, которых явно не достаточно для построения компенсационных уравнений. Поэтому последние включают изотопные уравнения широкого географического круга, что существенно затрудняет их интерпретацию и заставляет говорить только о некоторой тенденции.
Рис.10. Распределение параметров уравнений δ34S(В)= Sδ34S(А) + А. На рис пары соответствуют изотопным системам (А – В).
Основные результаты описаны в [26, 36]. Результаты выявления и анализа компенсации отражены на рис. 10 и в таб. 2. Во всех случаях Хп– халькопирит, Пр– пирротин, Пи– пирит, Сф– сфалерит, Гл–галенит.
Таблица 2. Сводные данные по значениям исходных параметров в сульфидах.
|
Минер.пара |
Гл – Сф |
Пи – Сф |
Пр – Пи |
Пи – Хп |
Пр – Хп |
||||||
|
Минералы |
Гл |
Сф |
Пи |
Сф |
Пр |
Пи |
Пи |
Хп |
Пр |
Хп |
|
|
δ34S |
1 |
20,44 |
21,45 |
2,06 |
0,64 |
3,83 |
3,66 |
5,84 |
4,90 |
1,73 |
1,97 |
|
2 |
0,637 |
2,016 |
10,7 |
9,63 |
|
|
|
|
|
|
|
III. Неоновые системы. По литературным данным были изучены изотопы 20Ne, 21Ne, 22Ne преимущественно в метеоритах, а также в некоторых земных объектах.
Рис.11. Компенсационная диаграмма для изотопов: А- изотоп 21Ne; Б- для изотопа 22Ne
Результаты анализа отражены в работе [15]. В этой работе впервые использованы представления о компенсационных уравнениях. Большое количество материала позволило практически для каждого метеорита построить изотопные уравнения вида iC = bi(1/Ne) + Bi и iC = ai 20C + Ai, а вслед за этим – компенсационные уравнения. Здесь Bi – радиационная, а Ai – примесная компоненты. На рис. 11 приведена компенсационная диаграмма распределения параметров изотопных уравнений, характеризующих 21Ne и 22Ne. На осях координат откладывались значения a*i = 1/ai и A*i = -аi* Ai.На всех диаграммах выделяются две группы изотопных составов Ne c различными параметрами: Ne1- 20Со: 21Со: 22Со= 32,60: 32,47: 34,67; Ne2= 87,065: 1,71: 8,77 соответственно.
IV. Свинцовые системы. Наиболее изученная система. Она описана в работах [10, 11, 14, 31]. При их описании использовались представления о компенсационных уравнениях. Примечательно, что именно в этом случае была детально построена теория решения обратной задачи о смешении - задачи об источниках вещества. Был изучен широкий круг геологических образований, радиоактивных (настураны , цирконы, монациты и другие) и нерадиоактивных минералов (галениты, полевые шпаты, халькопириты), а также магматические, метаморфические и осадочные породы. В результате было установлено, что концентрации изотопов описываются уравнениями iC = bi/Pb + Bi и iC = ai 204C + Ai. Полученные уравнения отражают смешение радиогенного и примесного (обыкновенного) свинцов. По этим данным построены и компенсационные диаграммы: на рис. 12А - для пород и настуранов, на рис. 12Б- для галенитов.
Рис.12. Компенсационная диаграмма для настурана (А) и галенита (Б).
V. Силикатные системы и окислы. Изучено распределение δ18O в минералах различных состава, возраста, генезиса, местонахождений: биотите Bi, мусковите Mu, калишпате Kf, альбите Al , кварце Q, магнетите Mt. Общие особенности распределений δ18O в минералах отражены в работах [8, 9, 13, 26,27, 32- 35]. Имеющиеся материалы позволяют провести для этих систем анализ уравнений компенсации. Все эти данные отражены на рис. 13-14.
Рис. 13. Распределение параметров δ18О(Б)= А δ18О(А) + В.
В таб. 2 приведены параметры полученных уравнений компенсации. Эти данные характеризуют состав вещества в объектах, послуживших источником вещества для минералов. Состав воды минералов рассчитывался по температурным уравнениям для Тиз из [8, 33, 34].
Таблица 2. Результаты определения параметров уравнений компенсации
|
|
δD |
δ18O |
δ18O |
|||||||||
|
Bi1 |
-91,9 |
4,05 |
Mu |
7,8 |
Bi |
5,4 |
Al |
10,0 |
Kf |
11,8 |
Mt |
-2,7 |
|
H2O |
-109,6 |
3,75 |
|
7,2 |
|
5,1 |
|
6,4 |
|
11,1 |
|
- |
|
Bi2 |
-53,1 |
4,69 |
Q |
10,5 |
Q |
11,4 |
Q |
12,0 |
Q |
12,9 |
Q |
13,3 |
|
H2O |
-70,8 |
4,39 |
|
8,8 |
|
10,8 |
|
11,4 |
|
12,3 |
|
12,7 |
Рис. 14. Распределение параметров δD(М)= А δ18О(М) + В в системах (X-Y). X = δ18O; Y = δD. А – мусковит: Б – биотит.
ГЕОХИМИЧЕСКИЕ СИСТЕМЫ
Здесь описываются распределения породообразующих элементов в минералах из горных пород различного состава. Из литературных источников заимствованы результаты силикатных анализов биотитов (около 1223 анализов), пироксенов (около 1033 ан.), гранатов (около 1000 ан.) и оливинов (около 140 ан.). Для этих минералов разбивка на виды не проводилась. По этим данным проводилось объединение проб в индивидуальные выборки по регионам и породам. В связи с широким присутствием названных минералов в разнообразных породах различных регионов из-за недостатка аналитических данных также оказалось сложным выделение однородных индивидуальных выборок. При этих построениях проводилась жесткая фильтрация анализов: из выборки выбрасывались пробы, существенно отклоняющиеся от корреляционной прямой и так, чтобы показатель R2, отождествляемый с коэффициентом корреляции, приближался к единице. Практически принимались выборки с R2 ³ 0,95. Довольно часто в остатках выявлялись дополнительные корреляционные зависимости. В случае выявления связей по нескольким элементам, учитывались только связи, установленные по одним и тем же пробам. Затем строились геохимические уравнения вида Эл = A(Fe) + B для каждого минерала, где Эл- кристаллохимический коэффициент соответствующего элемента, (Fe) – то же для железа Fe+2; A и B – постоянные коэффициенты (далее функция Эл = f(Fe)). Поскольку в основе работы лежит выявление линейной зависимости, то проверялась распространенность этой зависимости в минералах. Так в биотитах, если игнорировать выдуманную связь Si- AlVI, уравнение Mg = f(Fe+2) установлено в 68,75% от общего количества выявленных связей, Mn = f(Fe+2) – 12,5%, Ca = f(Fe+2) - 6,25%; Na = f(Fe+2) - 7,5%; K = f(Fe+2) -5% (всего 80 уравнений). В гранатах: Mg = f(Fe+2)- 63,5%; Ca = f(Fe+2) – 20,6%; Mn = f(Fe+2) – 15,9% (63 уравнения). В пироксенах: Mg = f(Fe+2)- 55,0%; Ca = f(Fe+2) – 30,0%; Na = f(Fe+2) - 10,0%; Mn = f(Fe+2) – 5,0% (160 уравнений).
Ниже приводится краткое описание результатов для каждого минерала.
БИОТИТ. Большой материал представлен в работе [3] по гранитоидам,
Здесь проведена детальная разбивка пород по гнейсам и сланцам Белоруссии, составу, месту отбора, структуре и минеральным ассоциациям. Выделено около 25 индивидуальных выборок, по которым строятся четко выраженные компенсационные диаграммы (рис.14). Эти закономерности сохраняются и на других объектах. Так, в карбонатитах для пары (Fe+2 – Mg) уравнение компенсации имеет вид В= -1,9811А + 0,517.
На рис. 14 приведена сводная компенсационная диаграмма для пары (Fe+2 – Mg) для всех кислых силикатных пород, куда входят гранитоиды, гнейсы, сланцы, диориты, сиениты и др. для всего земного шара. На рисунках диаграммы иллюстрируют наличие компенсации в биотитах практически для всех элементов. Если построить сводную компенсационную диаграмму для всех изученных элементов и минералов (биотит и гранат), не отделяя их друг от друга, то все точки кучно ложатся на общую прямую (рис.17).
Рис. 14. Компенсационные диаграммы распределения параметров А и В в уравнении Mg = A(Fe+2) + B биотитах кислых пород Белоруссии (на 24 атома О).
Рис. 15. Компенсационная диаграмма для кальция в биотитах.
Рис. 16. Компенсационная диаграмма для марганца и натрия в биотитах.
Рис. 17. Сводная компенсационная диаграмма по всем породам, минералам и элементам (А) и по сланцами гнейсам (Б).
Рис.18. Компенсационные диаграммы для гранатов эклогитов (А) и кимберлитов (Б)
Рис. 19. Компенсационные диаграммы для связи Ca = А(Fe+2) + В в гранатах.
Рис. 20. Компенсационная диаграмма для связи Mn = А(Fe+2) + В в гранатах.
ГРАНАТЫ пироксенитов, перидотитов, кимберлитов, лерцолитов, эклогитов, гнейсов, гранитогнейсов, гранитов, сланцев и др. пород из различных регио-нов мира. Установлены корреляци-онные зависимости вида Эл = А(Fe+2) + В, где Эл- Mg, Ca и Mn. На рис. 18- 19 приведены некоторые диаграммы для связи Mg = А(Fe+2) + В; на рис.19- Ca = А(Fe+2) + В в сланцах и гнейсах, а на рис.20 - Mn = А(Fe+2) + В в лампроитах, эклогитах, гнейсах и др.
Рис.21. Компенсационная диаграмма для связи Mg = А(Fe+2) + B в пироксенах базальтов, сиенитов и гнейсов.
Рис.22. Компенсационная диаграмма для связи М = А(Fe+2) + B (М = Ca, Na, Mn) для пироксенов в разных породах
ПИРОКСЕНЫ отбирались из эклогитов, сиенитов, пироксенитов, перидотитов, толеитов, габбро, мраморов, гнейсов, скарнов и др. Выделено 48 выборок, из них 6 выборок по ортопироксенам, остальные - из клинопироксенов. Выявлены связи вида Эл = А(Fe+2) + B, где Эл- Mg, Ca, Mn, Na. На рис. 21- 22 приведены компенсационные диаграммы для этих связей.
Рис.23. Компенсационная диаграмма дляультраосновных пород.
ОЛИВИН из основных и ультра-основных пород (базальты, дуниты, серпентиниты, перидотиты, габбро, лерцолиты) и метеоритах. Всего создано 11 выборок, в которых выявлена только связь Mg = А(Fe+2) + B. Одна из групп выборок показана на рис. 23.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ЯВЛЕНИЯ КОМПЕНСАЦИИ.
Проведенный беглый обзор явления компенсации показал его высокую распространенность. Это явление характерно для образований широкого круга и характерна как для различных объектов фазовой, химической, генетической и другой природы.
Связь между прямыми и их компенсационными преобразованиями известна давно [5, стр. 63]. В работе [31] приведено наше доказательство вида этой связи. Значения координат точки кроссовера определяются теоремой 1: прямые вида Y = АkX +Вk. характеризуют распределение компонентов X и Y в k выборках. Если они образуют пучок прямых, то параметры Аk и Вk этих прямых описываются уравнением прямой линии вида Вk = gАk + G, где g= Хо, G= Yo. Параметры Хо и Yo являются координатами (тангенциальными или плюккеровыми [5]) этой точки пересечения (кроссовера). В теории диффузии [4, 41] это уравнение называется компенсационным уравнением.
При анализе явления компенсации используются связи между параметрами двух компонент. В общем случае можно выделить группы параметров компенсационных уравнений:
1). Параметры имеют различные физические смыслы, а значит и различные размерности. Примером являются зависимости концентраций элементов от Т, Р и пр.
2). Параметры, концентрационные значения которых, откладываемые по осям координат, имеют одну и ту же размерность. Как правило, сюда относятся зависимости между элементами в вещественных (геохимических) полях. Выделяются следующие группы исходных уравнений связи:
1. Простая форма компенсация. В этом случае изучается распределение параметров в одной и той же среде (матрице). Здесь выделяются два подмножества исходных уравнений:
1а. Оба параметра имеют равную размерность. Например, в биотитах можно рассматривать множества, описываемых функцией Mg= f(Fe), т.е. связывают друг с другом концентрации (или кристаллохимические коэффициенты) магния и железа.
1б. Параметры имеют различные размерности, а значит и различную физическую природу. Примером являются зависимости концентраций элементов от Т, Р и пр., например, уравнения изотопных и геохимических геотермометров, а также уравнения диффузии.
2. Сложные формы компенсации. Выделяются подмножества:
2а. Гомогенная компенсация - имеется несколько параметров одинаковой размерности. Изучается их поведения в объектах (средах) одной и той же природы. Например, диффузия большого количества элементов в одной и той же матрице. Или поведение кристаллохимических коэффициентов в объектах одной природы (в одних и тех же породах), расположенных в различных географически местах, например, кристаллохимические коэффициенты Fe и Mg в биотитах из различных гранитных или гнейсовых массивов.
2б. Гетерогенная компенсация - поведение элементов в разных средах, например, коэффициенты диффузии одного элемента в различных матрицах (породах). Или поведение кристаллохимических коэффициентов в разных минералах, привязка их к породам не обязательна. Например, связь вида Fe= f(Mg) можно рассматривать в биотитах из разных пород, но можно ее рассматривать в разных минералах, в которых имеются эти элементы, например, в биотитах, гранатах, пироксенах и пр.
2в. Одна из координат общая для нескольких систем. Например, для биотита или граната зависимости могут иметь вид Mg = f(Fe) и Ca= f(Fe). Здесь уже мы имеем как минимум три оси координат, хотя их в указанном варианте может быть и больше, например, к указанным зависимостям можно прибавить зависимость Mn= f(Fe). Сюда же можно отнести диффузионные уравнения для элементов в одной и той же матрице, геохимические геотермометры с различными отношениями концентраций элементов в левой части и т.д.
2г. Система объектов, в которых физический смысл и размерность параметров на осях координат могут быть различными, хотя формально по этим данным также можно выявлять компенсационные зависимости. Интерпретация параметров этих компенсационных уравнений затруднительна, такие зависимости мы будем условно называть квази- (или псевдо) компенсационными.
Явления компенсации хорошо интерпретируется в геохимических полях на основе представлений о смешении компонентов. В общем, любую величину можно назвать смешанной, или составной, если ее можно некоторым образом разложить минимум на две составляющие компоненты. Ясно, что это возможно в случае, если компоненты, во- первых, имеют одинаковую размерность; во- вторых, если они суммируемы. Не все физические величины обладают свойством суммирования (аддитивности). Действительно, если в окрестность некоторой точки A поместить тела с массами m1 и m2, нагретыми до температур Т1 и Т2 соответственно, то можно утверждать, что масса m системы будет равна сумме масс компонентов m = m1 + m2, но температура Т системы не подчиняется этому правилу, т.е. Т ≠ Т1 + Т2. Здесь будет выполняться неравенство Т1 >(<) Т > (<) Т2. Таким образом, масса тела является абсолютно аддитивной величиной, тогда как Т этим свойством не обладает. То же можно сказать о давлении, скорости и других геофизических параметрах. Поскольку уравнение диффузии содержит температуру, то на основе представлений о смешении диффузионная компенсация решения, видимо, не имеет.
Говоря о механизме смешения, необходимо выделить два их вида.
А). Смешение проявляется в механическом добавлении в систему частиц вещества этой или другой природы. Источники этих веществ мы называем источниками уровня I [19, 25, 31]. Это – наиболее распространенный вид смешения. Примером систем, в которых этот вид смешения наблюдается, являются смешение водных потоков, а также свинцовые системы, изученные ранее [10, 11, 14, 31]. В свинцовой системе добавление вещества осуществляется за счет радиоактивного распада с увеличением общего количества Pb. Для анализа системы производят искусственное приведение концентраций компонентов к 100%. Тем самым переводим систему в систему второго вида. Эта операция оказалась достаточно результативной. Уравнения смешения описаны в [19, 25, 31]. В целом установлено:
Теорема 2: в индивидуальных выборках относительные концентрации iС свинца описываются уравнением (4).
iС = bi/Pb + iСо1 (4)
Теорема 3: в индивидуальных выборках относительные концентрации iС изотопов Pb связаны уравнением (5).
iС = ai 204C + Ai. (5).
Б). Смешение осуществляется за счет замещения частиц одного вещества частицами другого вещества. Типичный представитель этого вида замещения - изоморфное замещение. В этом случае параметры системы не изменяются, например, при замещении магния железом в биотитах и отсутствии других изоморфных элементов сумма кристаллохимических коэффициентов (далее КК) не изменяется, т.е. КК(Fe) + КК(Mg) = ККo= const (постоянная кристаллохимической ячейки КХЯ). На примере распределений магния и железа в кристаллохимической ячейке минерала доказана Теорема 4: пусть концентрация железа изменяется в пределах от Fe1 до Fe2, т.е. Fe1 > Fe > Fe2; магния – Mg1 > Mg > Mg2. Тогда при смешении этих компонентов их распределение описывается уравнением Mg = -AFe + В [37a].
Таким образом, теоремы (2) – (4) свидетельствуют, что при смешении компонентов их распределение описывается уравнением прямой линии. В свинцовых системах в связи с наличием априорно известного независимого источника свинца (радиоактивный распад) возможно и определение исходных параметров. В этом случае свободный член уравнения (5) определяет состав радиогенного свинца, а в уравнении (4)–примесного свинца в источнике уровня II. В геохимических системах эти параметры не определимы. Дальнейший анализ будем вести на примере наиболее изученной Pb-изотопной системы.
В геологии известны факты, когда из одного источника (например, магматического очага) образуются несколько объектов (гранитных интрузи-вов). Такая же ситуация существует и в изотопной геохимии: из некоторого источника выделяются порции Pb, которые сами становятся источником свинца уровня I. Такие источники мы называем источниками вещества уровня II. Этот уровень отражает состав радиогенных и примесных Pb, общих для нескольких индивидуальных выборок. Анализ распределений изотопов позволяет оценить этот источник. Он опирается на предположение: если две выборки, распределение Pb в которых описывается уравнениями iС1 = a1 jC1 + A1 и iС2 = a2 jC2 + A2, содержат Pb состава (iСo2, jCo2) из одного (общего) источника, то прямые, описываемые названными уравнениями, пересекутся в точке состава (iСo2, jCo2) [37a].
Примеры расчетов этих параметров приведены в работах [10, 11, 14, 31]. В практике геохронологических исследований весьма часто используются приведенные параметры и приведенные уравнении вида Y = γX + Γ, где Y = 207С/204С, Х = 206С/204С и т.д. - приведенные параметры. Эти системы, как и все системы с приведенными параметрами, бедны по содержанию, но и к ним применимы представления о компенсационных уравнениях. В работе [31] приведено обоснование этого вывода. В принципе то же можно сказать и об уравнениях с изотопами легких элементов (δ13С, δ18О, δ34S и т.д.); выше они описаны в разделе о карбонатных, сульфидных, силикатных системах. Такая же ситуация и с отношениями элементов в минералах: во многих случаях выполняется явление компенсации.
Таблица 7. Уровни глубинности источников вещества по свинцово-изотопным данным.
|
Источники уровня I. |
Источники уровня II. |
Источники уровня III. |
|
iСM = bi/PbM + iCo1 (1a) iСM = ai 204CM + iCp1 (1б) |
iСo1 = -(1/Pbo2) + iCo2 (2a) iCp1 = -(204Co2)ai + iCo2 (2б) |
iСo2 = di 204Co2 + iCp3 (3a) и т.д. |
Таким образом, при работе в вещественных (геохимических [7]) полях явление компенсации находит удовлетворительное объяснение с позиций теории задач об источниках вещества (или задачи о смешении). Материалы В.В. Смирный [40] свидетельствуют, что они применимы и к анализу распространенности минералов. Параметры компенсационных уравнений в источниках уровня II позволяют определять концентрации компонентов, которые обычными способами не определяются.
Таблица 8. Сводная таблица компенсационныхуравнений в системе Fe- Mg.
|
№№ п.п. |
Мине-ралы |
Породы |
N |
g |
G |
|
1 |
Сpx |
Габбро |
5 |
-0,1187 |
0,904 |
|
2 |
|
Щелочные породы |
6 |
-0,7934 |
0,156 |
|
3 |
|
Гнейсы |
|
-0,4654 |
0,561 |
|
|
G = 1,1069g + 1.0483; R2 = 0,996 |
||||
|
4 |
Bio |
Гнейсы |
6 |
-2,1024 |
2,581 |
|
5 |
|
Гнейсы |
13 |
-2,0402 |
2,579 |
|
6 |
|
Граниты Белоруссии |
8 |
-2,1064 |
2,361 |
|
7 |
|
Гранитоиды |
7 |
-2,6483 |
1,855 |
|
8 |
|
Гранитоиды |
4 |
-1,6754 |
3,470 |
|
|
G = 1,6051g + 5.9632; R2 = 0,9123 |
||||
|
Примечание: Минералы- Cpx- клинопироксены, Olv – оливин, Sch-шпинель. N –количество выборок, g и G – параметры компенсационных уравнений В = gА + G. |
|||||
БИКОМПЕНСАЦИЯ.
Таким образом, можно выделить множество индивидуальных выборок, вещество которых поступает из одного источника; этим выборки становятся замкнутыми. Подобные выборки мы назовем родственными, а самую группу будем называть семейством родственных выборок (или семейством выборок).
Примеры семейств выборок установлены в свинцовых системах и приведены на рис. 11. Здесь выделяется семейство выборок, представленных породами, и семейство, сложенное уранинитами урановых месторождений. Как видим, по параметрам компенсационных уравнений они различаются, говоря о различии источников их питания.
Два семейства выявлены в неоновых системах [15] (рис. 10). Большой материал собран по распределению элементов Mg, Fe, Ca, Na и K в биотите, гранате, пироксене, оливине. Таким образом, каждое семейство выборок характеризуется парой чисел. Поэтому при наличии более двух семейств выборок возможно построение компенсационных уравнений, названных бикомпенсационными уравнениями, а самое явление – бикомпенсацией.
Рис. 24. Диаграмма бикомпенсации в биотитах и клинопироксенах разных пород (гран-д - гранодиориты, Щел.пор.- щелочные породы (сиениты и пр.) ).
Множество семейств выборок, описываемое уравнением бикомпенсации, образуют надсемейство выборок. Понятно, что в таком случае мы изучаем параметры вещества еще более глубокого уровня III.
Рис. 25 Диаграммы бикомпенсации для гранатов.
Для свинцовых систем в результате изучения решения задачи о смешении (источниках вещества) получены уравнения, представленные в табл.7, которые позволяют устанавливать исходные параметры смешивающихся компонентов на разных по глубинности уровнях. В геохимических системах исходные компенсационные уравнения приведены в табл. 8, а на рис. 24–диаграммы бикомпенсации для биотита и клинопироксена; на рис. 25 – для гранатов, на рис. 26–бикомпенсационная диаграмма для кальцитов. Согласно им в гранатах и кальцитах выявляются по два рода выборок. В геохимических системах интерпретации бикомпенсации затруднена. По существу уравнение бикомпенсации тождественно уравнениям индивидуальных выборок, и угловой коэффициент бикомпенсационного уравнения согласно теореме 4 отражает только отношение долей смешивающихся элементов в кристаллохимической ячейке в минерале источника уровня III. Однако для кальцитов можно говорить о температуре образования кальцитов в источниках уровня III. Так для
Рис. 26. Диаграммы бикомпенсации для кальцитов.
первого рода выборок кальцита она оценивается в 180оС, для второго ~ 270оС. Родовой источник описывается точкой пересечения (на рис.26 обведено кружком) диаграмм надсемейств с координатами: δ18Oоо ≈ -30‰ (SMOW) и δ13 Cоо ≈ -5‰ (PDB).
Эти данные позволяют оценить источники изучаемых элементов. Все значения изотопного состава углерода не информативны. Такие значения установлены также в составе газов Марса, Луны и других планет. Установлено наличие весьма лёгкого кислорода (δ18Oоо ≈ -30‰ (SMOW)). Такие значения более типичны для воды, в которой величины δ18O могут достигать значений до -40‰ [43]. На Земле в твёрдых фазах они отсутствуют. Но в некоторых метеоритах [Лаврухина, 1992] отмечено значение δ18O = -65‰. Близкие величины обнаружены в тонкозернистых межпланетных частицах. Анализ образцов КА-та "Генезис" (Genesis) показал, что на Солнце в СО2 концентрация 16О (отношение количества 16О к общему количеству кислорода) существенно выше, чем на Земле [42]. Таким образом, изначально кислород земных карбонатов, видимо, мог иметь космогенную(?) природу.
Литература.
1.Бобровник И.И., Митьков Л.Г., Царяпкин А.М. Оценка скоростных параметров разреза по данным промыслово-геофизических исследований. //."Проблемы нефти и газа Тюмени". Вып.57. Тюмень, 1983.С.11 – 15.
2.Бокштейн Б.С., Бокштейн С.З., Жуховицкий Л.А. Термодинамика и кинетика диффузии в твердых телах. М.: Металлургия, 1974, 280 с.
3. Булкин Ю.С. Состав биотита гранитоидов как индикатор условий породообразования.- Минск: «Наука и техника», 1989.
4. Катлинский В.М. Новые закономерности твердофазной диффузии./ Тугоплавкие металлы, сплавы и соединения с монокристаллической структурой. М.: Наука, 1984. С.62- 69.
5. Корн Г., Корн Т. Справочник по математике. М.: Наука. 1978. 831 с.
6. Кузнецов К.Е. К оценке явления самодиффузии в бинарных соединениях./ «Физико-химия эндогенных процессов. Новосибирск: Наука, 1979. С. 129.
7. Макаров В.П. Вопросы систематики геохимических ореолов и аномалий. //Изв. ВУЗ. Геология и разведка, 1983, 6. С. 52- 57.
8. Макаров В.П. Последовательность кристаллизации породообразующих минералов по изотопным данным. Тез. докл. /Симпозиум «Геохимия магматических пород». М.:ГЕОХИ, 1991. С.98.
9. Макаров В.П. Об определении условий образования породообразующих минералов. Тез. докл. /Симпозиум «Геохимия магматических пород». М.: ГЕОХИ, 1991. С. 82-83.
10. Макаров В.П. Особенности распределения относительных содержаний изотопов свинца.//Советская Геология, 1991, 6. С.56 – 61.
11. Макаров В.П. Об определении возраста урановых минералов.//Геология и геофизика, 1991, 4. С.76- 81.
12. Макаров В.П. О некоторых условиях образования высокотемпературных карбонатов. Тез. док. /Симпозиум «Геохимия магматических пород». М.: ГЕОХИ, 1993.
13. Макаров В.П. О проявлении диффузии при образовании породообразующих минералов по изотопным данным. Тез. док. /Симпозиум «Геохимия магматических пород». М.: ГЕОХИ, 1993.
14. Макаров В.П. О природе обыкновенного свинца в минерала.// Отечественная геология, 1994, 4. С. 67- 76.
15. Макаров В.П. О стадийности образования неона в метеоритах.//Отечественная геология. 1995. 4. С.58- 66.
16. Макаров В.П. К проблеме использования диффузии в петрологии. /Геохимия магматических пород. М.: изд. ГЕОХИ, 1995.
17. Макаров В.П. О некоторых условиях образования высокотемпературных карбонатов. Тез. док./ Конференции «Эволюционно- геологические факторы рудообразования и прогноз месторождений полезных ископаемых». М.:ВИМС, 1996. С. 72.
18. Макаров В.П. К проблеме использования диффузии при геологических исследованиях. /Конф. «Новые идеи в науках о земле». Тез. док. М.: МГГА, 1997. С. 228.
19. Макаров В.П. Некоторые математические вопросы решения задачи о смешении при изотопных исследованиях. Тез. докладов. /IV Международная конф. «Новые идеи в науках о Земле». – М.: изд. МГГА, 1999. С.257- 258.
20.Макаров В.П. Об универсальности распространения в природе «уравнения компенсации»./IV Междун. конф. «Новые идеи в науках о Земле». Тез. докл. М.: изд. МГГА, 1999. Т.1. С.257 - 258.
21. Макаров В.П. О геотектонической позиции и экзогенном источнике вещества карбонатитов (по изотопным данным). Тез. док. /XXXII тектон. совещ. «Тектоника, геодинамика и процессы магматизма и метаморфизма». М.:ГИН, 1999, Т.1. Сс. 387-390.
22. Макаров В.П. Некоторые особенности образования низкотемпературных карбонатов по изотопным данным./Литолог. совещ. «Литология и полезные ископаемые центр. России». Воронеж: ВГУ, 2000. С.52- 53.
23. Макаров В.П. Некоторые условия образования низкотемпературных карбонатов по изотопным данным.Тез. док. /Совещание «Проблемы литологии, геохимии и рудогенеза осадочного процесса». М.:МГУ, 2000, Т.1. С.433- 437.
24. Макаров В.П. Об участии экзогенных карбонатов в процессах высокотем-пературного минералообразования по изотопно-геохимическим данным. Там же. С. 437- 440.
25.Макаров В.П. Некоторые математические вопросы решения задачи о смешении при изотопных исследованиях. /IV Междунар. Конф. «Новые идеи в науках о земле». Избран. докл. М.: НИА «Природа», МГГА, 2000. С. 136- 142.
26. Макаров В.П. Некоторые условия образования сульфидов рудных месторождений по изотопным данным./ Конф. «Геологическая служба и минерально-сырьевая база России на Рубеже ХХI века.- СпБ, ВСЕГЕИ, 2000.
27. Макаров В.П. Температура образования породообразующих минералов. Тез. докл. /Междунарародная конференция «Кристаллогенез и минералогия». Санкт-Петербург, Сп-БГУ, 2001.
28. Макаров В.П. К проблеме использования диффузии при анализе мине-ралов./ «Кристаллогненезис и минералогия». Междунар. конф. Тез.докл. Санкт- Петербург, Сп-БГУ. 2001.
29. Макаров В.П. К проблеме учета диффузии при петрологических исследованиях. /Электронный научно-информационный журнал РАН, 1(21)`, 2003. URL http://www.scgis.ru/russion/cp1251/h_dgggms/1_2003/informbul-1_2003/mineral-16/pdf.
30. Макаров В.П. Условия образования экзогенных кальцитов по изотопным данным. Тез. док. /VI Уральское литологическое совещание «Карбонатные осадочные последовательности Урала и сопредельных территорий: седименто-, литогенез, минерагения». Екатеринбург, 2004. С. 93- 95.
31. Макаров В.П. Основы теоретической геохронологии. /XII научный семинар «Система «Планета Земля»».- М.: РОО «Гармония строения Земли и планет», 2004. С. 228- 253.
32. Макаров В.П. О механизме выделения минералов: магматические и метаморфические породы. Тез. докл. /Ежегодный семинар по эксперимен-тальной минералогии, петрологии и геохимии. 21.04.2004. URL: www.scgisru/russion/cp1251/h_dgggms/1-2004/informbul-1_2004/izotop-2.pdf. URL: //www.geokhi.ru/conference/annotat-05-05.doc.
33. Макаров В.П. Изотопные геотермометры. /Materiály II mezinarodni vĕdecko – praktická conference «PERSPEKTIVNI NOVINKY VĔDY A TECHNICI – 2005», Díl 7. Praha – Dnĕpropetrovsk, Publishing house Education and Science s.r.o., 2005. P.53 – 67.
34. Макаров В.П. Изотопные геотермометры./Материалы XIII научного семинара «Система планета земля» (Нетрадиционные вопросы геологии)./ М.:РОО «Гармония строения Земли и планет». 2005. С. 93- 115.
35 Макаров В.П. О некоторых условиях кристаллизации минералов мафиче-ских пород и метеоритов. Тез. докл. /Семинар «Геохимия магматических пород». М.: ГЕОХИ. 2005. URL: //www.alkaline2005.narod.ru.
36. Макаров В.П. О механизме выделения минералов. 2. Сульфиды рудных месторождений. /Ежегодный семинар по экспериментальной минералогии, петрологии и геохимии». Тез. докл. М.: ГЕОХИ, 2006. URL: //www.scgis.ru/russion/cp1251/h_dgggms/1-2006/informbull_thesis-doc.zip.
37. Макаров В.П. «Уравнение компенсации»- новый метод изучения петрохимических особенностей высокотемпературных образований (на примере биотита). /Семинар «Геохимия, петрология, минералогия и генезис щелочных пород». Миасс, 2006.
37а.Макаров В.П. «Явление компенсации» - новый вид связи между геологическими объектами. / Материалы I Междун. Научно-практической кон-ции «Становление современной науки-2006». Т.10. Днепропетровск: Наука и образование, 2006. С. 85-115.
38. Макаров В. П.Некоторые свойства геохимических геотермометров./XIV научный семинар «Система «Планета Земля»». (Нетрадиционные вопросы геологии) /М.: РОО «Гармония строения Земли и планет», 2006.
39. Малкин В.И., Могутнов Б.М. Самодиффузия щелочных ионов в силикатных расплавах. //ДАН, 1961, 141, 5. С. 1127- 1134.
40. Смирный В. В. Закономерности минерального состава мраморов и кальцифиров тетерево-бужской свиты (Украина)/ Труды ВСЕГЕИ, Ленинград, 1968, Т.125. С.179- 190.
41. Сорокин Н.Д. Оценка параметров диффузии атомов в минералах. //Геохимия, 1992, 5. С. 619.
42. http://www.dialog-21.ru/news/digest.asp?id=142317
43. Институт геоэкологии РАН, Санкт-Петербургское отделение/URL: http://www.hge.pu.ru/index.php?option=com_content&task= view&id= 549&Itemid=99999999
44. Макаров В.П. Вопросы теоретической геологии. 12. Основы теории решения задачи об источниках вещества./ Материалы международной конференции. «Научные исследования и их практическое применение. Современное состояние и пути развития-2008». Одесса: «Черноморье», 2008. Т.17. С.12 - 47.
45. Макаров В.П. О свойствах углеводородного вещества- источника нефти./Сб. Литология и геология горючих полезных ископаемых. Екатеринбург: изд-во УГГУ, 2011, 5921). С.95 – 108.
46. Сурков А.В. Атлас форм самородного золота (золотин). М.: СтудиА, 2000. 63 с. ISBN 5-89010-017-3.
47. Сурков А.В. Новое в изучении песчано-алевритовой компоненты россыпей и осадочных пород. М.:Издатель Е.Разумова, 2000. 287 с. ISBN 5-93513-008-4/
48. Макаров В.П, Сурков А.В. Вопросы теоретической геологии. 6. О форме золотин в россыпях. /Международная научно-практическая конференция «Нау-чные исследования и их практическое применение. Современное состояние и пути развития ‘2007». 1-15 окт. 2007. Одесса: Черноморье, 2007, Т.16. С. 38 47.
49. Макаров В.П. , Сурков А.В. О форме золотин в россыпях./«Литология и геология угольных ископаемых», Екатеринбург, Урал. гос.горный ун-т, Т. 3(19), 2009. С.74 – 79.
50.Романовский С.И. Седиментологические основы литологии. Л.: Недра, 1977. 408 с.
Примечание:
Источник: Макаров В.П. Явление компенсации» - новый вид связи между геологическими объектами. /Материалы I междун. Научно-практич. конференции «Становление современной науки-2006». Т.10. Днепропетровск: Наука и образование, 2006. С. 85-115. С добавлениями.