Вопросы теоретической геологии.
10. К проблеме механизма перемещения и
осаждения твердого вещества из водных потоков.
В.П. Макаров
Российский государственный геологоразведочный университет, г. Москва
Вопросы происхождения осадочных горных пород и определение обстановок осадконакопления при проведении геологических исследований являются ведущими, поскольку правильно установить генезис – это понять закономерности развития осадочной оболочки Земли, а потому корректно прогнозировать месторождения, связанные с осадочными породами и локализованные в них.
В формировании осадочных толщ существенную роль играют транспортировка и отложение слагающих толщи компонентов. Эти процессы подчиняются законам механики, в частности, гидродинамики. В технике такие процессы изучает наука о гидротранспорте [4]. Перенос осадков водными потоками можно назвать природной формой гидротранспорта. При изучении этих вопросов как относительно самостоятельные типы задач выделяются прямая и обратная задачи. Прямая задача заключается в выяснении особенностей распределения параметров зерен в рыхлых отложениях под влиянием априорно известных физико-механических параметров среды, в которой осуществляются перенос и отложение этих зерен. К решению этого типа задач относятся различные эксперименты и аналитические исследования, например [3], прежде всего выполняемые гидрологами, механиками, специалистами по гидродинамике и гидравлике. К этому типу задач относится и задачи седиментологии, изучающей особенности образования осадков в конкретных природных условиях. К последним относятся многочисленные исследования Н.М. Страхова [15].
Крупные работы и эксперименты по изучению гидродинамики переноса русловых отложений, формирующих аллювиальные образования, проведены гидрологами и океанологами в связи с анализом особенностей построения плотин, дамб и пр. ([3,13]; Л.Г. Лойцянский; В.М. Гончаров; А. М. Годен; Дж. Гриффитс; Л. Прандтль; Я. Церебровский и др.). Работами В.П. Зенковича и других изучены особенности переноса и отложения осадков морских побережий. Получены основные уравнения зарождения, переноса и отложения осадков. Изучены их взаимоотношения с водными потоками, количество переносимого вещества, возникновение ламинарного и турбулентного движений водного потока. Показано, что первичной формой перемещения зерна является скачок, хотя детально форма не изучена. В общих чертах рассмотрен механизм истирания частиц, ведущий к их округлению и уменьшению размера.
К обратным относятся задачи по определению физико-механических параметров среды, в которой осуществляются перенос и отложение этих зерен, по особенностям распределения параметров зерен в реальных рыхлых осадках. Поисками решений этого типа задача занимаются, в первую очередь, литологи. Этот тип задач не совсем точно и достаточно расплывчато называют «установлением генезиса изучаемого объекта».
В основе всех выводов лежит представление о кинетической энергии движения частицы E= Мv2/2 (М- ее масса, v - скорость движения). Поскольку М = Vρ (V- объем, ρ- плотность частицы), то понятна роль этих непосредственно измеряемых параметров в изучении механики образования осадков. Эта механику иногда называют литодинамикой [10, 12].
Ранее решение многих задач литологии опиралось на изучение данных гранулометрии на основе ситового анализа рыхлых и литифицированных осадочных горных пород. Метод не оправдал надежд исследователей [12, 16], так как разные по «генезису» осадки давали сходные распределения гранулометрии классов. Однако, другие, более надёжные методы решения этих задач ни гидрологами (седиментологами), ни литологами не созданы.
К сожалению, механики и геологи (литологи) не различают эти задача и механически используют решения прямых задач для анализа особенностей строения и сложения осадков. На самом же деле решение обратных задач не сводится к решению прямых задач, хотя и опирается на них. Задачи у них прямо противоположные. Наличие решения прямых задач говорит только и только о том, что решение обратной задачи возможно и существует и его необходимо искать самостоятельными методами. Кроме того, любое решение прямой задачи говорит только о вероятной (!!) природе осадочного объекта. В следствие игнорирования указанных обстоятельств выводы литологов о природе осадочных толщ являются поверхностными и примитивными, а в целом в литологии процветает махровый застой.
В целом, выделяются три основных периода увлечения гранулометрическим методом. Первый всплеск приходится на предвоенные годы (В.П. Батурин, 1947; Л.Б. Рухин, 1947 и др.) становления литологии и накопления материала, первых попыток использования представлений литодинамики. Незнание литологами основ последней привели к непониманию необходимости этих громоздких исследований, а качественный характер работ - отказу от этих измерений и заменой их выделением гранулометрических фракций ситовым методом (В.П. Батурин, 1947; Л.Б. Рухин, 1947).
Второй всплеск приходится на пятидесятые - шестидесятые годы. В это время в литологию внедряются представления гидродинамики отложений механических осадков, наступает период увлечения уравнением Стокса [14, 15], заимствованное у Engelgardt (1939 - 1940 г. г.) и с тех пор бездумно кочующее из одних работ в другие ([14, 15]; В.П. Батурин, 1947). Однако это увлечение имело поверхностный характер, давая только качественную картину распределений минералов. Поэтому и здесь осталась неясной необходимость точных измерений, сохранился ситовой метод, не смотря на все возрастающий застой в его развитии, обусловленный качественностью получаемых выводов и не возможностью оценить количественные характеристики геологических процессов.
Третий период (в конце восьмидесятых- девяностых годов) связан, в первую очередь, с работами А.В. Суркова [16] по изучению россыпей золота. Он возобновил измерения параметров A, B и C, веса золотин и других минералов. Им показана порочность ситового метода, игнорирующего различие форм зерен, существенно искажающего не только весовые соотношения между фракциями, но и чистоту их выделения. Стало ясно, что ситовой метод нанес удар по развитию литодинамики. В то же время измерения А.В. Суркова создали базу для изучения условий образования осадков на основе представлений литодинамики, опираясь на анализ соотношений между плотностью и размерами минералов. Заметим к тому же, что идеи гидротранспорта [4] не только не нашли дорогу в литологию, но литологи не знают и не хотят знать о существовании этого важного для литологов раздела гидравлики.
Несмотря на полученные результаты, использование их для решения обратных задач литологии затруднительно. Кроме явного не желания литологов заниматься этими проблемами, сюда накладываются и другие обстоятельства:
1) громоздкость уравнений;
2) осадки рассматриваются как однородные по минеральному и плотностному составу образования;
3) анализов распределения в потоках различных минералов, представляющих интерес как прямой объект исследования, весьма мало;
4) абсолютизирована величина плотности воды ρв = 1, хотя минералы осаждаются не из чистой воды, а из смеси воды и твердого материала (взвеси), которая имеет свои значения плотности и вязкости [5, стр. 147]. В гидравлике такие смеси относятся к аномальным объектам;
5) почти нет работ по определению вязкости взвесей в широком интервале концентраций твердого вещества.
В связи с этим остался не освещенным ряд проблем формирования осадочных отложений. Не изучены условия взаимодействия частицы и вмещающей водной среды: роль трения, влияние формы частицы на дальность транспортировки; не изучен характер влияния среды накопления осадков на связь между размером, плотностью и формой осадочных частиц, искажены соотношения между формой частицы и окатанностью и т.д.
В настоящее время выделяются две основные гипотезы формирования осадочных отложений. Одной из немногих идей механики, используемых для решения задач литологии, является гипотеза осаждения минерала в стоячей жидкости, использующая уравнение Стокса (В.П. Батурин, 1947; [14, 15]):
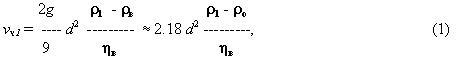
где vч1-скорость осаждения частицы диаметром d и плотностью ρ1 в воде с плотностью ρо и вязкостью ηв. В теории движения русловых потоков, например, [3], эта гипотеза играет большую роль. Уравнение Стокса используется для решения многих обратных задач:
1) определение вязкости вмещающей частицу жидкости (вискозиметрия);
2) в литологии – определение гидравлической крупности частиц; выделение глинистых фракций; объяснения особенностей распределения минералов в осадке по зависимости линейных размеров зерна от его плотности. Так при сравнении параметров распределений кварца КВ и магнетита МТ в предположении, что vКВ=vМТ, Л.Б. Рухин [14] и Н.М. Страхов [15] установили, что при ρМТ > ρКВ обычно dМТ < dКВ, соответствуя качественным особенностям их распределения в реальных осадках. На основе этого они сделали вывод об обоснованности использования уравнения Стокса при анализе строения осадков. Ревизия этих данных не подтверждает это суждение:
1). Не обоснована сама возможность применения представлений Стокса для изучения механизма разделения минералов в реальном осадке при попадании в жидкость некоторого объема сыпучего тела с произвольными соотношениями размеров и плотностей зерен.
2). Уравнение Стокса использовалось при условии, что плотность воды ρв = 1. Это означает, что концентрация частиц в воде настолько мала, что не влияет на плотность системы вода–осадок (взвеси), и противоречит заключениям Рухина и Страхова, что основные процессы формирования осадка проходят в обогащенной твердым материалом пограничной зоне, примыкающей к границе вода – осадок.
3). Проверка уравнения Стокса на других объектах не позволяет делать подобные заключения. Так например, в [16] описано распределение параметров кварца КВ (ρ = 2,65 г/см3), граната ГР (ρ = 3,70 г/см3) и циркона ЦР (ρ = 4,70 г/см3). Для КВ при нормальном распределении размеров зерен по оси С модальное значение dКВ = 0,29 мм, для ГР –dГР = 0,22 мм, для ЦР – dЦР = 0,16 мм. Подстановка данных для КВ и ГР в уравнение Стокса приводит к значению ρo1.кг = 1,23 г/см3, свидетельствующее, что процесс распределения минералов проходит во взвеси. Однако, для пары (КВ– ЦР) ρo1.кц = 1,85 г/см3; а для (ГР– ЦР) – ρo1.гц = 2,58 г/см3. В первом приближении зерна морфологически подобны, но оценки ρo1 значительно разнятся, говоря о недостатках метода.
В основе гипотезы 2лежит представление о гидротранспорте, опирающееся на взаимоотношения потока и перемещаемых им наносов [4]. Там выделяются напорные потоки, двигающиеся в близ горизонтальном направлении. В этом случае выделяются скорость vтр трогания частицы, заполонившая всю литологическую литературу, и скорость vк критическая, о которой почти не говорят. Под скоростью трогания понимают «среднюю скорость, при которой твёрдое начинает перемещаться волочением по стенке трубы». Под критической скоростью «понимают минимальную среднюю скорость потока, при которой ещё не происходит выпадения осадка на стенку трубы.» [4, стр.146]. Ясно, что реальные скорости, определениями которых и должны заниматься литологи, значительно превышают эту критическую скорость. Указанные скорости выражаются следующим образом:

Здесь Vч- объём частицы, F- миделево сечение, т.е. проекция тела на плоскость, нормальную к линиям течения потока; f- коэффициент трения частицы о стенку трубы; Схт – коэффициент лобового сопротивления тела, учитывающий влияние стенок трубы на обтекание тела (частицы) потоком; Сут – коэффициент подъёмной силы; g – ускорение силы тяжести; ρч – плотность тела частицы; ρ- плотность воды. Утверждается, что Схт ≠ Сут. Обе формы отличаются только значениями сопротивлений. К сожалению и здесь наблюдается застой в развитии теории гидротранспорта в изучаемом направлении. Так указанные представления почти дословно повторяются авторами [4] с 1970 г и далее в работах 2001 г. [6], отличаясь только шрифтом публикации и типом бумаги, на которой они напечатаны. В работе [5] также рассмотрены вопросы о соотношениях между скоростью vч частицы в потоке и скоростью vп самого потока, и получено уравнение

где φ –фактор формы (коэффициент сопротивления). По М.А. Великанову [3] vч ≈ vп. Это уравнение использовано нами при анализе вопросов осадкообразования [17], хотя по своей структуре они тождественны уравнению (3) и отличаются только формой их выражения. Обе гипотезы дают близкие качественные картины распределений минералов по плотности и размеру зерен. Следовательно, необходим другой подход для оценки этих гипотез с точки зрения лучшего объяснения распределений минералов по плотности и размерам. Уравнения (1) и (4) включают параметры ρ и d, измеряемые в реальных условиях. Поэтому для решения задачи эти параметры должны быть использованы в качестве главных параметров и связаны функционально. Тогда для первой гипотезы получаем уравнение гиперболы ρ= 0,46vчh/d2 + ρo1, (в общей форме ρ = α/d2 + ρo1); для второй ρ = (φ vч2ro2)/19,6d + ρo2, где d= V/F (в общей форме ρ = β/d + ρo2).
Вхождение параметра vч в коэффициенты при аргументе говорит, что все частицы двигаются с одинаковыми скоростями. Полагая l = 1/d или l* = 1/d2, получаем уравнение прямой линии ρ = βl + ρo1 (или ρ= αl* + ρo2) (α и β - постоянные). Следовательно, анализируемые точки должны располагаться на этой прямой. Одна из таких диаграмм, иллюстрирующая выполнение этого условия, приведена на рис.1. Эти уравнения и будут служить основой оценки двух гипотез: ближе к реальному распределению осадков будет та гипотеза, для которой величина ρoi будет ближе к значению плотности воды ρв = 1.
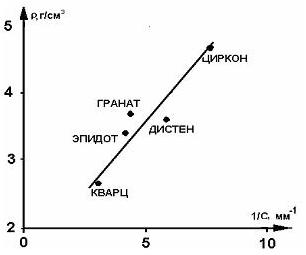 Рис. 1. Характер связи между плотностью минерала и размером зерна по оси С.
Рис. 1. Характер связи между плотностью минерала и размером зерна по оси С.
Для решения задачи использованы результаты изучения в локальной точке пляжных песков (прибойная зона пляжа «Зимний берег» в Горле Белого моря [16]) песчано-алевритовой размерности, ранее отмученных и освобождённых от более крупной компоненты, по методике, описанной в [17]. С небольшими добавлениями эти материалы приведены в табл.1 и на рис.2. Все измерения параметров зёрен проведены А.В. Сурковым (МГРИ). Северная часть Белого моря (Абрамов берег) наиболее штормовая и характеризуется сильным волнением. В часы наибольшего развития приливно- отливных морских течений их скорости достигают 3 м/сек. Сильные течения р. Мезень имеют скорость > 3 м/сек [10]. Баланс наносов обусловлен поступлением обломочного материала от разрушения Абрамового, Зимнего и других берегов. Песчаные осадки на пляжах маломощны. В таблице 2 приведен состав гранулометрических фракций песков Абрамова берега. По данным табл. 1 зерна имеют форму, приближенную к призмоиду. Хотя в [11] говорится, что в кварце длинная ось располагается вдоль оси co, но из таблицы видно, что связь формы зерен с параметрами кристалла более сложная. Независимо от характеристик кристалла связи между параметрами осей зерен имеют вид A= 0,993B + 0,017 (коэффициент корреляции КК= 0,997), C= 0,482B + 0,00521 (КК= 0,944) или A/B = 2,687(C/B) – 0,288.
Согласно вышесказанному d= V/F= С. Тогда по первой гипотезе ρ = 0,0003774/С2 + 2,5; по второй– ρ= 0,0431/С + 1,34.
Полученные данные позволяют оценить скорости движения наносов. Для первой гипотезы α= 0,46uчη= 0,0003774. Данных по величине η для взвеси нет.
Таблица 1. Результаты грануло- минералогического анализа проб пляжа «Зимний берег» в Горле Белого моря [16].
|
Мине-рал
|
r,
г/см3
|
Синго-ния
|
Параметры решетки, Å
|
Средние размеры, cм
|
|
аo
|
bo
|
co
|
A
|
B
|
C
|
|
Циркон
|
4,7
|
Тетраг.
|
6,59
|
6,59
|
5,94
|
0,034
1
|
0,019
0,56
|
0,0130,38
|
|
Гранат
|
3,7
|
Кубич.
|
11,84
|
11,84
|
11,84
|
0,053
1
|
0,039
0,74
|
0,023
0,43
|
|
Дистен
|
3,62
|
Трикл.
|
7,10
|
7,74
|
5,57
|
0,048
1
|
0,028
0,58
|
0,017
0,35
|
|
Эпидот
|
3,4
|
Монокл.
|
8,94
|
5,61
|
10,23
|
0,052
1
|
0,034
0,66
|
0,024
0,46
|
|
Кварц
|
2,65
|
Тригон.
|
4,903
|
4,903
|
5,393
|
0,065
1
|
0,048
0,74
|
0,033
0,51
|
|
Среднее
|
|
|
|
0,504
1
|
0,035
0,667
|
0,022
0,437
|
Приведём некоторые замечания к уравнению (4).
1. Коэффициент φ отражает величину лобового сопротивления. Но величина сопротивления трения в формулу не входит, она учитывается только в уравнении (2). Необходимо выделение как минимум двух видов трения: трение частиц с водой потока и трение частиц между собой, поскольку во взвеси с повышенной концентрацией твердых частиц возникают постоянные взаимоотношения между частицами. Это трение изучено очень плохо, поэтому недоучёт его является ошибкой. Что касается первого вида трения, то оно видимо не велико, поскольку при попадании частицы в воду на поверхности частицы образуется удерживаемый молекулярными силами монослой воды. Этот монослой играет роль смазки, сводящей трение между водой и частицей к трению между слоями воды. Малое значение трения между слоями воды отражается малым значением вязкости воды, равной 0,01 пуаз. Далее под коэффициентом φ будем пониматьэффект, учитывающий сумму сопротивлений лобового и трения.
2. Параметр Vч/F отражает линейные размеры частицы. Обобщение, например, [9], измерений В.А. Суркова показало, что в зернах почти всех изученных минералов (кварц, магнетит, циркон и др.) песчано- алевритовой размерности в >99,0% A > B > C, т.е. зерна относятся к типоморфной группе призмоидов. Поскольку F – проекция тела частицы на плоскость, то здесь возможны два крайних варианта положения тела зерна, исключая кувыркание, т.е. вращение зерна в потоке:
а) длинная ось А перпендикулярна линиям тока и
б) эта ось располагается вдоль этих линий тока.
Тогда в первом случае F ≈ АВ (или АС)и Vч/F ≈ С (или В). Во втором случае F ≈ ВС и Vч/F ≈ А. Естественно, первый случай соответствует перекатыванию частицы в потоке при перемещении, способствующему истиранию частиц.
Таблица 2. Гранулометрический состав рыхлой фракции береговых отложений [10].
|
№№ проб
|
Фракции, мм (в % по весу).
|
|
>2
|
2–1
|
1– 0,5
|
0,5– 0,25
|
0,25– 0,1
|
0,1– 0,05
|
0,05– 0,01
|
<0,01
|
|
38
|
7,2
|
5,7
|
11,1
|
53,2
|
21,6
|
1,2
|
–
|
–
|
|
39
|
–
|
–
|
4,8
|
10,0
|
22,4
|
14,4
|
18,6
|
29,8
|
|
166
|
–
|
–
|
2,6
|
5,6
|
11,0
|
13,6
|
12,6
|
54,6
|
|
167
|
–
|
–
|
–
|
1,2
|
4,8
|
17,8
|
58,4
|
17,8
|
для воды ηв = 0,01 пуаз. Для этого значения ηв vч = 8 м/сек, Если принять для взвеси условно η= 1, то vч = 0,08 м/сек.
Для второй гипотезы β = φvч22 ρo2/19,6= φvч22/14,73= 0,0431.Проведем оценку величины φ, опираясь на измерения параметров потоков на конкретных участках. По [3] φ = gRi/v2, где R = гидравлический радиус; для плоских потоков R= h, h- глубина и v- скорость потока; i - гидравлический уклон. Для отмелых берегов Балтийского моря [1] i = 0,016; v = 0,8 м/сек и h =2 м; поэтому φ= 0,245, а vч= 1,61 м/сек; для φ ≈ 1 vч= 0,8 м/сек.
Информацию о структуре взвеси дает рис. 2, показывающий различие площадей кривых, соответствующих каждому минералу. Поскольку отбор проб проводился независимо от состава минерала, то соотношение площадей, показывает соотношение минералов в осадке. По распространенности минералы образуют ряд- кварц: эпидот: гранат: диопсид: циркон = 5,2: 3,8: 2,4: 1,8: 1.
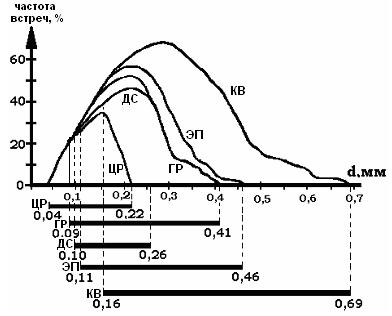 Рис.2. Структурные спектры минералов в россыпях пляжей Белого моря. Минералы: КВ - кварц; ЦР – циркон; ГР – гранат; ДС- дистен; ЭП- эпидот. Черные прямоугольники отражают основания спектров.
Рис.2. Структурные спектры минералов в россыпях пляжей Белого моря. Минералы: КВ - кварц; ЦР – циркон; ГР – гранат; ДС- дистен; ЭП- эпидот. Черные прямоугольники отражают основания спектров.
Эти значения обратно пропорциональны плотностям минералов. Средневзвешенная плотность осадка 3,24 г/см3.
Объемная доля S взвеси в потоке (мутность) вычисляется по формуле S = 100(ρoi – 1)/ρм. Так как средняя плотность взвеси ρм = 3,24 г/см3, то для первой гипотезы S= 46%, для второй - S= 17%. По М.А. Великанову [3] Sмах = 50%, для речных наносов Sмах= 38%, для наносов более тяжелых, чем песок, гравий, глина, величина Sмах <38%. Следовательно значение S = 17% является более реальной величиной в отличие от S = 46%.
Таким образом, ρo1 = 2,5 г/см3, ρo2 = 1,34 г/см3. Поскольку последнее ближе к плотности воды, то второй гипотезе отдано предпочтение.
Измерений плотности взвеси в реальных условиях не достаточно. Концентрация взвеси на Балтийском море достигает 22,53 г/л (соответствует r= 1,0225 г/см3). На р. Cыр- Дарье (С.Т. Алтунин, 1959) мутность колеблется около 1- 2 г/л, увеличиваясь в паводке до 50 г/л (ρ = 1,050 г/см3). В нижнем течении р. Аму- Дарьи [13] мутность взвешенных наносов (фракция d< 0,1 мм) колеблется в пределах 2,36- 3,32 г/л (r= 1,00236 – 1,00332 г/см3). На р. Мезень [10] средняя мутность воды 30 г/м3, временами достигая 8 г/л. Высокие значения концентрации взвеси наблюдаются в суспензионных потоках [8], в них количество мути бывает >100– 300 г/л (ρ= 1,10 – 1,30 г/см3). На оз. Байкале [8] плотность наносов изменяется от 1,6 до 2,0 г/см3.
Скорость начала трогания (срывающая скорость) частиц размером 0,75 – 1,0 мм равна 0,05– 0,105 м/сек [7]. Приведение в движение всей массы наносов этой размерности происходит при скоростях в 1,3 раза больше (Н.В. Разумихин, 1959), т.е. при 0,065– 0,14 м/сек. Реальные скорости движения осадков значительно больше. В спокойной обстановке скорость течения вод в районе отмелых берегов Балтийского моря [1] изменяется от 0,08 до 1,0 м/сек. Скорость течения воды у дна моря – 0,15 – 0,83 м/сек. Измеренная скорость движения в воде песчаных наносов (частицы размером 0,5 – 0,75 мм) – 0,84 м/сек [7]. По В.П. Зенковичу в районе Керченского полуострова в спокойной обстановке скорость перемещения отдельных меченых частиц диаметром 0,25 мм равна 3 – 4 см/сек. В других местах она может достигать 22 – 23 см/сек при скорости ветра 6 м/сек и волнении 2 балла. В Белом море в этих условиях скорость течений не более 14 см/сек. В то же время у береговых зон Балтийского моря при сильных волнениях величины придонных скоростей достигают 4,73 м/сек [1]. Установлено [2], что с усилением волнения скорость перемещения меченых песчинок приближается к скоростям течения самой воды, показав роль штормовых течений в массовом переносе песка.
Таким образом, поток осадков на побережье Белого моря характеризуется параметрами ρо2 = 1,34 г/см3 и vч= 1,61 м/сек, мутность потока – 17%. Эти параметры не соответствуют потокам осадков пониженной плотности в спокойных условиях. Подобные параметры характеризуют случай больших скоростей, когда «частицы оказываются в полувзвешенном состоянии и все движение приобретает характер медленного течения грязевой массы …» [3]. Эти скорости характерны для сильных штормовых волнений, которые и создают условия для формирований этой селеподобной массы.
Таким образом, по значениям плотности ρо взвеси и ее количеству (мутность) наиболее приемлема гипотеза, что распределения минералов по плотности и размерам зерен и по переносимой массе определяются условиями их переноса и осаждения из движущейся взвеси, т.е. смеси воды потока и переносимого им рыхлого материала в условиях сильных штормовых волнений. Эту взвесь называют дисперсоидом [3], суспензионным потоком или турбидидами [8]. Полученные данные вместе с результатами исследований условий осаждения песчаного материала в Чудском озере [17] показывают, что для анализа условий осадкообразования не применимы представления, описываемые уравнением Стокса.
Дополнение 1.
При анализе переноса осадочного материала необходимо учитывать следующие обстоятельства:
1.Перемещение осадочного материала осуществляется как в декартовом пространстве, так и во времени. Это позволяет записать выражение М = f(x,t), где М- масса переносимого материала, х- координата, вдоль которой происходит это перемещение; t- время.
2. Осадочный материал поступает в бассейн вследствие разрушения некоторого исходного геологического тела, выполненного рыхлым материалом, причём количество выносимого материала пропорционально количеству материала в геологическом теле. Это позволяет записать следующие исходные уравнения:
dM/dx = - axM (1); dM/dt = - atM (2).
В случае стационарности процесса переноса, т.е. при dM/dt– 0, получаем классическое решение в виде экспоненциалльной зависимости [3].
Объединив уравнения путём удаления общего параметра М, получим
dM/dx = (ax/at)(dM/dt). (3)
Для выявления природы этого выражения продифференцируем его по х, затем его же по t. В результате получаем
(d2M/dx2) = (ax/at)(d2M/dtdx);
(d2M/dxdt) = (ax/at)(d2M/dt2).
Полагая (d2M/dtdx) = (d2M/dxdt) и исключив общие члены, приходим к выражению
(d2M/dx2) = (ax/at)2(d2M/dt2). (4)
Это уравнение является «простейшим гиперболическим уравнением» [19, с. 23] в дифференциальной форме. Это уравнение ещё называют уравнением струны [19].
В принципе этот результат не нов. Ещё М.А.Великанов [3], анализируя перенос осадочного материала водными потоками, использовал гиперболические уравнения. Но он не привел вывода этих уравнений, исходя из физической природы процесса переноса рыхлого твёрдого вещества. С нашей точки зрения уравнения (1) и (2) и определяют физическую сущность гиперболического уравнения (4).
Для определения физического смысла коэффициента (ax/at) левую часть уравнения (2) умножим и разделим на величину dx. В результате получаем (dM/dx)/(dx/dt) = - atMилиv(dM/dx)= - atM, где v= (dx/dt)- скорость перемещения вещества. Введя сюда уравнение (1), получим (- axM)v = - atM, откуда v = at/ax. Исходя из этого, уравнения (3) и (4) приобретают вид
dM/dx = (1/v)(dM/dt), (3а)
d2M/dx2 = (1/v)2(d2M/dt2). (4а)
Дополнение 2.
Анализ механизма перемещения твердого осадочного материала позволяет выделить следующие закономерности этого перемещения.
1. Пассивный характер перемещения зерен в водных потоках. Водный поток толкает попавшее в него зерно и за счет этого происходит его перемещение.
2. Размерные параметры зёрен в общем случае образуют геометрическую прогрессию, соответствуя логнормальному закону распределения размерных параметров зерен [18]. Основание прогрессии изучено недостаточно и практически не известно.
3. Дальность перемещения обратно пропорциональна размерам зерна (З). В первом приближении это следует из анализа кинетики движения потока. Кинетическая энергия переноса единицы объема водного потока описывается уравнением E = mv2/2, где m– масса этой единицы, v– скорость движения потока. Для зерен З1 и З2 величины кинетических энергий определяются из выражений E1 = m1v12/2 и E2 = m2v22/2. Так как энергия потока передается переносимым зернам, то можно записать, что Е = Е1 = Е2. Тогда для обоих зерен выполняется соотношение m1/m2 = v22/v12. Поскольку m= ρV, то ρ1V1/ρ2V2= v22/v12. Для частиц одного состава, в которых ρ1 = ρ2, имеем V1/V2= v22/v12, т.е. вперед уходит зерно меньшего размера. Это объяснение обладает одним недостатком: оно не учитывает взаимодействие зерна с потоком при перемещении; в этом выводе по умолчанию предполагается, что зерна, получив от потока некоторую долю его энергии, далее двигаются независимо от потока. Но это не так. Зерно, двигаясь с меньшей скоростью относительно потока, представляет собой преграду; преодолевая ее, поток передает зерну дополнительную энергию, искажая полученную выше картину. Кроме того, не объясняется логнормальное распределение размерных параметров зерен.
Итак, при переносе осуществляется энергетическое взаимодействие потока и зерна. В термодинамике взаимодействие между веществами описывается через химический потенциал m; его величина отражается равенством m = mо + RTlnC, где С – концентрация компонента в соединении, mо – некоторая постоянная. Пассивный характер переноса зерна отобразим преобразованием m = mо + RTln(1/C) = mо - RTlnC. Если общая масса взвеси равна М, а масса зерна из этой взвеси– m, то С = m/M. Это - безразмерная величина, если взвесь сложена зернами одного состава. Тогда mо1= mо2 и для зерен с массами m1 и m2 имеем m1- m2= Dm12= (mо1- RTlnC1) - (mо2- RTlnC2 ) = RTln(C2/C1). Далее:
1. Зная С и m, для зерен одного состава получаем Δμ 12= RTln(V2/V1). Если V2 > V1, то m1- m2> 0 и m1 > m2, т.е. зерно мėньших размеров обладает бόльшим потенциалом. Для зерен З1, З2, З3 (V1 < V2 < V3) имеем Δμ12= RTln(V2/V1) и Δμ23= RTln (V3/V2). Если Δμ12= Δμ23, то V2/V1= V3/V2, т.е. параметры образуют геометрическую прогрессию.
2. Подставляя V1/V2 = v22/v12 в формулу разности потенциалов, получаем m1 - m2 = 2RTln(v1/v2). Выше установлено, что при V2 > V1 имеем m1 > m2, откуда v1 > v2. Значит, меньшая частица с более высоким потенциалом переносится с бόльшей скоростью и на бόльшее расстояние относительно бόльшей частицы. Таким образом, меньшая частица бόлее активна, чем частица с большими размерами.
Химический потенциал, отражая взаимодействие двух соединений, можно назвать потенциалом притяжения. В потоках перемещаемых зерен происходит их дифференциация, в результате чего зерна, разделяясь, удаляются друг от друга. Поэтому разность Δμ12 можно назвать потенциалом отталкивания.
ЛИТЕРАТУРА,
1.Айбулатов Н.А.. Долотов Ю.С.. Орлова Г.А. и др. Некоторые черты динамики отмелого песчаного берега. /Исследование гидродинамических и морфодина-мических процессов береговой зоны моря. М.: Наука, 1966. С. 38- 103.
2.Болдырев В.Л.. Зенкович В.П. и др. Применение люминесцентных меченых песков для изучения перемещения морских и речных наносов. /Процессы развития и методы исследования прибрежной зоны моря. М.: Наука, 1972. С. 4- 26.
3.Великанов М.А. Динамика русловых потоков. М.: Гостехиздат. т. I, II. 1955.
4.Гейер В.Г. и др. Гидравлика и гидропривод. М.: Недра, 1991. 331 с.
5.Гостинцев К.К. Метод и значение гидродинамической классификации песчано- алевритовых пород при поисках литологических ловушек нефти и газа. /Методика прогнозирования литологических и стратиграфических залежей нефти и газа. Л.: издание ВНИГРИ, 1981. С. 51- 62.
6. Гудилин Н.С. и др. Гидравлика и гидропривод. М.: издание МГУ, 2001. 519 с.
7. Жуковец А.М. Моделирование процесса перемещения морских песчаных наносов. / Исследование гидродинамических и морфодинамических процессов береговой зоны моря. М.: Наука, 1966. С. 104- 111.
8. Карабанов Е.Б.. Фиалков В.А. Подводные каньоны Байкала. Новосибирск. Наука. 1987. 104 с.
9. Макаров В.П., Сурков А.В. Вопросы теоретической геологии. 5. О форме зёрен в аллювиальных отложениях./Материалы междун. научно- практической конфер. «Научные исследования и их практическое применение. Современное состояние и пути развития ’2007». Одесса: «Черноморье», 2007. С.27-38.
10.Медведев В.С. Схема литодинамики и баланс наносов северной части Белого моря. /Процессы развития и методы исследования прибрежной зоны моря. М.: Наука, 1972. С. 27- 53.
11.Петтиджон Ф. Дж. Осадочные породы. М.: Недра, 1981. 751 с.
12.Романовский С.И. Физическая седиментология. Л.: Наука, 1988. 239 с.
13.Русловые процессы. /М.: изд. АН СССР, 1958.
14.Рухин Л.Б. Основы литологии. Л.: Недра, 1969. 491 с.
15. Страхов Н.М. Осадконакопление в современных водоемах. М.: Наука. 1993.
16. Сурков А.В. Методика грануломинералогического анализа при изучении обломочный пород. // Изв. ВУЗ- ов. Геология и разведка, 1993. 3. С. 36- 43.
17. Сурков А.В.. Фортунатова Н.К.. Макаров В.П. Об условиях образования современных осадков Чудского озера по гранулометрическим данным.// Изв. ВУЗ-ов, Геология и разведка, 2005, 5, С. 60 – 65.
18. Мидлтон Г.В. Возникновение логнормального распределения частот в осадках. /Вопросы математической геологии. Л.: Наука, 1968. С.37- 45.
19. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972. 735 с.
Примечание; источник - Макаров В.П. Вопросы теоретической геологии. 10. К проблеме механизма перемещения и осаждения твердого вещества из водных потоков. //Международная научно-практическая конференция «Со-временные направления теоретических и прикладных исследований.» //Одесса: Черноморье, 2008, Т.23. С.44 - 56.
Рис. 1. Характер связи между плотностью минерала и размером зерна по оси С.
Рис.2. Структурные спектры минералов в россыпях пляжей Белого моря. Минералы: КВ - кварц; ЦР – циркон; ГР – гранат; ДС- дистен; ЭП- эпидот. Черные прямоугольники отражают основания спектров.