Диффузия. К проблеме использования при геологических исследованиях
Участие диффузии в процессах формирования геологических объектов известно давно. Наиболее полно, видимо, оно изучено в нефтегазовой геологии и гидрогеологии, где представления об этом явлении применяются для анализа условий существования нефтяных и газовых залежей и химического состава подземных вод [Дж.Хат,1982].
В разделах геологии рудого профиля эти представления используются слабо. Они применяются более - менее широко в геохронологии с целью изучения процессов миграции радиогенных изотопов и выяснения механизма формирования «дискордантости» и времени проявления наложенных процессов [L.O. Nicolaysen, 1961; G.R. Tilton, 1960; G.J. Wasserburg, 1963; G.W. Wetherill, 1963; Х.И. Амирханов, 1979; Г.Ш. Ашкинадзе, 1980; А.С. Батырмурзаев, 1982; С.Н. Вороновский, 1970; И.М. Морозова, 1971 [19] и др.].
При изучении условий образования рудных и силикатных систем использование представлений о диффузии носило характер теоретизированных рассуждений. Основной объем работ в этой области содержал только экспериментальные определения параметров диффузии либо в расплавах [E.B. Watson, 1981 (Ca, Sc, Cs, Na); R.K. Lowry at al, 1982 (Na, Cs, Sc, Ba, Mn, Co, Fe, Sr); C. Alibert et al, 1980 (Si, Ti, K, Fe, Ca, Mg, Na), В.Р. Малинин и др, 1982 (Na, K, Rb, Cs); М.Б. Эпельбаум, 1976, 1979 (SiO2, Al2O3, CaO, MgO, FeO, K + Na, Na2O, H2O) и др.], либо в минералах при различных температурах Т и давлениях Р: в полевых шпатах (Na, K, Rb, Cs [A. Jambou et al]), биотите, мусковите, кварце (M. Sneeringer et al, 1984; М.И. Кучер, 1971-1978; Х.И. Амирханов и др., 1978), либо в породах (обсидиан, риолит, базальт [M. Magaritz et al, 1978; В.В. Матиас и др, 1977]) и пр.
С целью корректировки изотопных геотермометров (ИГТ) а также решения задачи об источниках вещества определены диффузионные параметры стабильных изотопов некоторых легких элементов (СИЛЭ) (18О, 13С, 2Н) в кальцитах и доломитах [R.A.M. Haul еt al, 1955; T.F. Anderson, 1962, 1972; H.C. Urey еt al, 1951; В.М.Сергеев и др.,1978), полевых шпатах (B.J. Giletti еt al, 1975; S.R.Hart,1981), флогопите (B.J. Giletti at al, 1975), кварце (A.Choudhury at al, 1965;), периклазе MgO (Y. Oishi et al, 1960), воде (J.H. Wang, 1965; W.G. Deuser, 1972), жадеите (N.Shimizu at al, 1984), в газах СН4 и СО2 (А.М. Зякун и др., 1974) и др. Сводка этих данных приведена в [20].
Теория явлений переноса вещества излагается во многих работах (А.Н. Тихонов, А.А. Самарский,1972; А.И. Китайгородский, 1973 [6]; А.В. Лыков, 1978; Д.В. Сивухин, 1979 и др.). Практические вопросы определения диффузионных параметров изложены, например, в работах А.С. Батырмурзаева (1982,1984), Ю.А. Шуколюкова, М.И.Кучера и других исследователей.
Полное уравнение потока массы описывается дифференциальным уравнением J= -D(dC/dX) + vC, в котором С- концентрация вещества, v -скорость переноса массы. В нем первый член отражает диффузионную часть, второй - конвективную. Соотношения между ними определяются соотношениями между длиной l свободного пробега частицы и диаметром d канала, по которому происходит ее миграция. Если d >> l, то преобладает конвективное течение; если d соизмеримо с l - то диффузионное перемещение. Применительно к изотопам основное значение имеет диффузионная компонента. Основой механизм диффузии- поток вещества, т.е. масса вещества, проходящая через единицу площади, прямо пропорциональна отрицательному градиенту концентрации ([6], с.188). В математической форме этот поток массы описывается уравнением ([4], с.15):
∂C/∂t = -D(∇2C + (k(t)/T)∇2T + (k(P)/P)2P),
где ∇2- оператор Лапласа. Второй член правой части характеризует термодиффузию, третий- бародиффузию. В простейшем случае одномерной диффузии она описывается законами Фика [23]:
Здесь k- коэффициент пористости. Если k= 1, Т= const и D= const, то имеет место уравнение dC/dt = -Dd2C/dx2.
В более сложных случаях D зависит и от массы вещества, и от Т процесса. В последнем варианте выполняется уравнение Аррениуса (например, [2, 9]):
D = Do exp(-Q/RT),
где Do - предэкспоненциальный множитель; Q- энергия (энтальпия) активации, т.е. количество энергии, которую надо затратить, чтобы частица начала двигаться; R- универсальная газовая постоянная, Т-абсолютная температура. Иногда [28] используется выражение D= D*exp(ATпл/T), где Tпл- температура плавления вещества. Выявляется различие в интерпретации члена Q: либо свободная энергия (Малкин и дp.,1961), либо энтальпия [10]). Это в значительной мере определяется тем, как интерпретировать уравнение Эйринга [28] D= 2(kT/h) exp(ΔS/R) exp(-ΔH/RT), где ΔS - энтропия, а ΔH - энтальпия самодиффузии. Считается, что отношение Q/RT отражает долю частиц, ушедших в диффузионное путешествие.
В общем случае при учете влияния Т и Р имеем [3]
D(T,P) = Do(1-kP) exp(-Q/RT).
Теоретический расчет величины Dо затруднен. Для самодиффузии имеется выражение Do = koω a2 exp(ΔH/RTпл) (эмпирическая формула Диннеса, 1950 г. [8, стр. 153]), где ω - средняя частота колебаний атомов, для большинства кристаллов равная по порядку величие 10-13 cм-1 (дебаевская частота); k -численный множитель, зависящий от деталей геометрии диффузии; а- длина пути диффузии, принимаемая равной постоянной кристаллической решетки.
Вместе с этим известно, что для газов удовлетворительно выполняется соотношение (закон Грэхем) V/V*= D/D* = √(M*/M), где М и М*- молекулярные веса соответственно изотопно-легкой и тяжелой компонент [28, 29].
Для практических целей используются разложения решения уравнения диффузии в ряд Фурье. В простейшем случае для сферической симметричной диффузии на изотерме это решение имеет вид [1, 3]
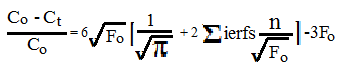
где Со и Сt- содержания компонента начальное и в момент времени t, Fo= Dt/a2 -критерий Фурье, t- время опыта, a- размер сферы или толщина пластины. При весьма малых значениях F это выражение упрощается, приобретая вид
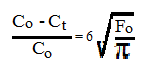
Выделяется несколько типов диффузий. По форме -это самодиффузия, описывающая миграцию компонентов одной природы, и взаимная диффузия (концентрационная) - миграция в некотором веществе (матрице) атомов другой природы (метки, диффунданта) и др. Наблюдается также поверхностная и объемная диффузии. По механизмам перемещения выделяются диффузия по вакансиям (наиболее распространенная), межузельная, гетеродиффузия и др. В настоящее время имеется очень большое количество определений 20] параметров [ диффузии, особенно в области металлургии сплавов и стекол. Это же относится и к определениям коэффициентов диффузии изотопных компонентов в природных материалах, например, изотопов O и C в кальцитах. Общей причиной подобного положения является существенная зависимость параметров диффузии от присутствия примесных компонентов, чем характеризуются многие минералы и породы. Например, N.H. Nachtrieb et al [28], изучая самодиффузию серебра, использует соотношение D(Ag) = Do + XD*, где D(Ag)- абсолютное значение, Do- значение в чистом Ag, Х- мольная доля примеси (Фп), D*- коэффициент самодиффузии в чистой примеси.
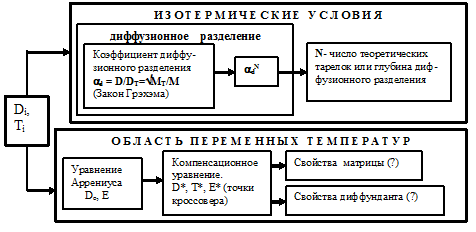
Рис. 1. Схема использования параметров диффузии.
Тем не менее, можно наметить обобщенную схему, представленную на (рис.1) [15], использования параметров диффузии. По этой схеме исходными являются единичные параметры диффузии Di, Ti для конкретных температур.
Дальнейшее обобщение возможно в двух направлениях.
-
Используется взаимодействие двух частиц, которое ведет к их разделению (диффузионное фракционирование). Применительно к природным процессам этих вопросов касались B. Daansgaard (1964 г.), J. Hoefs (1973), M.K. Stewart (1975), W.F. Giggenbach (1978), O. Mutsubaya (1979), H. Sakai и др., используя выражение α = (D/D')n; четкого смысла в параметр n они не вкладывали. A.A.Verbeck et al [31] использовал эти представления при описании миграции изотопов 39К и 41К в зоне контактового метаморфизма, применив понятие о теоретической тарелке.
Из соотечественников этой проблемой занимались А.М. Зякун и А.Д. Бондарь [4] для описания условий фракционирования изотопов C при миграции СО2 и СН4. Вклад в решении проблемы диффузии внесли также А.С. Батырмурзаев (1982) [2], И.А. Магомедов (1972) [10], И.М. Морозова (1974) [19] и др.
2. Дальнейшим развитием является использование представлений о теоретической тарелке, широко развитых в технологии промышленного разделения изотопов [21]. Под теоретической тарелкой понимается расстояние, при прохождении которого произойдет разделение частиц согласно отношению теоретических коэффициентов диффузии. Тогда общее разделение изотопов опишется равенством α = αдn, где величина n характеризует число теоретических тарелок. Сопоставление этих данных с результатами работ, например, W.Daansgaard [23] показывает сходство его выражения для описания разделения изотопов с выражением, используемом в промышленном разделении изотопов. Применительно к природным процессам понятие о количестве теоретических тарелок можно заменить понятием о глубине диффузионного фракционирования изотопов.
|
№№ п.п. |
Местоположение, страна, МПИ |
Поро- ды |
ТоС (изм) |
ИС |
ТоС (изот) |
Источник |
|
1 |
Nevada |
мр |
500- 600 |
СО2(0,7) - Н2О |
490 |
Taylor B.E., et al, 1977 |
|
2 |
Гренландия |
мр |
|
CH4(1)- H2O(0,5) |
300 |
Schidlowski M., et al, 1979. |
|
3 |
Енисейский кр. |
мр |
|
CH4(1) - H2O(0,5) |
300 |
Лапин А.В., др., 1986 |
|
6 |
Vermont |
мр |
300- 600* |
CO2(2) - CO2 |
400 |
Simon M.F., et al, 1970. |
|
7 |
АлПьпы |
мр |
450- 500 |
CO2(2) -CO2 |
400 |
Baertschi P., 1957. |
|
8 |
Альпы |
мр |
450- 500 |
CO2(2) - CO2 |
400 |
Baertschi P., 1957. |
|
10 |
Алдан |
мр |
400- 500 |
CH4 - CO2(1) |
540 |
Кулешов В.И., 1986. |
|
11 |
Коршуновское МПИ |
мр |
400? |
CH4 - CO2(1) |
580 |
Плюснин Г.С., др., 1981. |
|
12 |
Adironak |
мр |
600- 700# |
CH4 - CO2(1) |
600 |
Valley J.M., et al, 1981. |
|
17 |
Nevada |
ск |
500 |
CO2 (0,7)- H2O |
460 |
Taylor В.E., et аl, 1977. |
|
8 |
Коршуновское МПИ |
ск |
400 |
СН4(1) - Н2О(0,5) |
650 |
Пухнаревич М.М., др., 1985. |
|
20 |
Якутия, Эмельджак |
ск |
|
СН4 - Н2О(0,5) |
420 |
Кулешов В.Н.,1986. |
|
21 |
Федеровское МПИ |
ск |
|
СН4- СО2(1) |
600 |
Виноградов В.И., др. 1981. |
|
23 |
Hat Jron scarn d. |
ск |
150- 450 |
CН4(0,5)-CО2 |
450 |
Hall D.L., et al, 1988. |
|
Примечание: породы-ск-скарны; мр-мрамора; d-deposits; кр.- кряж. Темпе-ратуры, определены по геотермометрам: Т#- изотопным, Т*-геохимическим (по содержанию Mg). Т?-предположительные; МПИ-месторождение полез-ных ископаемых. Числа в скобках- глубина диффузионного фракциониро-вания: для воды- по кислороду, для СО2 – по углероду.
|
||||||
Исследования показали, что явления диффузии достаточно широко распространены в природе. В заведомо магматических образованиях кислого состава и карбонатитах эти явления не проявлены. Однако, они выявлены при образовании водосодержащих минералов (биотит, мусковит, амфиболы и др.) метаморфических пород широкого класса. Здесь диффундантом является *H2O (отмечен тяжёлый изотоп).
Среди других карбонатных образований диффузия сопровождает формирование широкого круга пород как органогенной, так и неорганогенной природы (кальциты биогенные, экзогенные, гидротермальные, мраморов, скарнов, кальцифиров). Фрагменты результатов этих исследований приведены в табл.1. Основными диффундантами являются *H2O, *CH4, *CO2, CO2*. Величина n (глубина диффузионного фракционирования) изменяется в пределах 0,03 - 1,5 (*H2O); 0,25 - 2 (CH4); 0,05 - 3 (CO2) [17].
3. Уравнения диффузии (УД) обобщаются через компенсационные уравнения (КУ) lnDo= gQ + G, в которых переменными уже являются параметры Do и Q. В первые эти уравнения появились при решении диффузионных задач. Ранее использовались представления о компенсационных уравнениях, описанные Н.Д. Сорокиным [20]. Компенсационным он называл уравнение вида lnDo = lnD* + Q/RT*. Здесь D* - коэффициент диффузии атомов всех элементов в данном теле, мигрирующих по одному закону. Однако у других исследователей [5, 18, 22], а также и у нас, используется другая, более понятная форма этого уравнения: lnDo= gQ + G. Основные характеристики этого типа уравнений приведены в [16, 17]. Координаты точки кроссовера – D* и T* (К. Крон, Т. Крон, 1978; В.П. Макаров, 2000): G = lnD*, g = -1/RT*.
Проведенные исследования с использованием базы данных (916 УД) по значениям Q и D, включавшей минералы (Т=200-800оС), расплавы пород (Т= 900-1440оС) и более простых систем (искусственные стекла) с переменным составом-(Y2O)(Y2O)4(SiO2), (Y2O)3(SiO2) (Y = K, Na, Li, Cs); (Y2O)(XO)4(SiO2) (X = Ca, Mg, Sr, Ba), стекла, сплавы и полупроводники (156 УД [7]) показали возможность построении компенсационных уравнений. Так сплавы имеет либо нечетко выраженные КУ, либо они не выявляются, либо зависимость между Q и Do имеет более сложный характер (рис.2.А). Здесь значительную роль
начинает играть концентрация примеси в матрице. На этом рисунке показана компенсационная диаграмма для диффузионных параметров вольфрама в сплаве с молибденом. Для силикатов как естественной, так и искусственной природы в большинстве случаев существуют компенсационные уравнения, среди которых выявлены два основных типа.
КУ-1. Наиболее важно распределение диффундантов в одной и той же матрице (рис.2Б-2, пример- андезит). Кроме того, сюда же попадают полупроводники [7], часть сплавов и др.
В табл.2 приведены КУ для полупроводников. В ней отмечены некоторые свойства диффундантов- тип примеси: акцептор (в тексте акц), донор (дон), нейтральный (нтр); вид диффузии: межузельная (му), диссоциативная (дц), поверхностная (пов). Всего создано 8 уравнений, которые получены по N=7 – 24 частным ДУ (табл.2). Эти УК охватывают 120 частных ДУ, или 77% общего их количества.
На рис. 3 представлены диаграммы компенсации по полупроводникам InAs, GaAs. Рисунок иллюстрирует характер поведения примесей в
|
Мат-рица |
g |
G |
R² |
N |
Диффунданты (метки) |
|
Ge1 |
4578 |
55252 |
0,9555 |
13 |
O,Ga,In(акц), P,As(дон),Sb(дон),Bi(дон),Au(му), Ge,Be,Sn. |
|
Ge2 |
4523 |
39262 |
0,9402 |
16 |
Tl,H,Fe,Ag(му),He,Co,Li(му),Na(му),Ag(му), 64Cu(му),Ni,Cu(акц). |
|
Si1 |
4786 |
74320 |
0,935 |
24 |
Si,Sn(нтр),Ge,B,Al(акц),Ga(акц),Ga,In(акц),As(дон), Sb(дон),Bi(дон),As,P,110Ag(му),Au(дц),Au(му),Cd. |
|
Si2 |
4953 |
48654 |
0,9648 |
20 |
Si,Ge,B,Al(акц),Cr,Fe,Li(му),Na(му),Na,K,Cu,Cu(му), 110Ag(му),Au(дц),Au(му),S,Zn. |
|
GaAs |
3659 |
63119 |
0,681 |
13 |
110Ag,Be,Mg,Cd,Zn,Ge,Sn,S,Se,Mn,As,Ga, |
|
InSb |
1875 |
41834 |
0,9715 |
20 |
In,125Sb,Sb,Ag,Ag(пов),Au,Li,Hg,Cd,Zn,Sn,Ge,S,Se,Te,Co,Fe. |
|
InP |
3167 |
48436 |
0,9456 |
7 |
In,P,Ag,Au,Cu,Cd, |
|
InAs |
3948 |
38616 |
0,9906 |
7 |
In,As,Ag,Au,Zn,S,Se. |
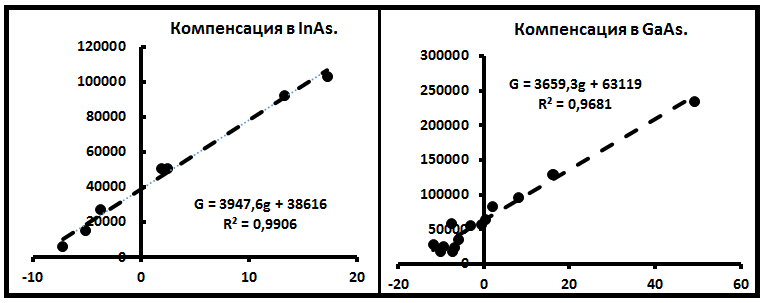
Рис.3. Диаграммы компенсации для полупроводников InAs, GaAs.
полупроводниках. Но имеется ещё одно явление. На рис.4 представлены диаграммы компенсации, на которых наблюдается по две достаточно хорошо выраженные выборки в одном веществе. Дополнительная информация о подобных выборках приведена в табл. 3. Особенность этих диаграмм состоит в том, что положение точек на них не зависит от механизма и вида диффузии, типа кристаллической решётки минерала - матрицы. Следовательно, интерпретация параметра lnD*, данная Н.Д. Сорокиным, недостаточно корректная.
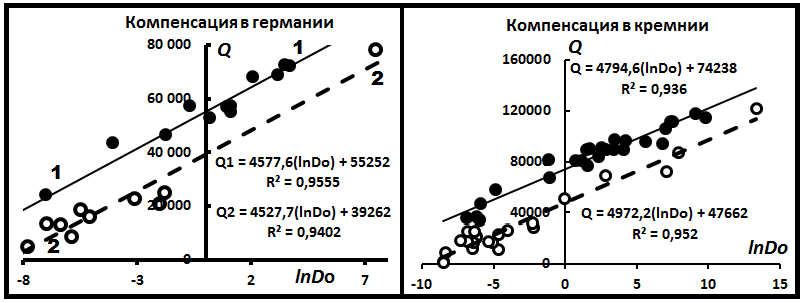
Рис.4. Диаграммы компенсации для полупроводников Ge, Si.
На рис.5 показана диаграмма бикомпенсации [16], построенная по данным табл.2. Выделяются нескольких выборок, одна из которых с учётом расшифровки параметров G и g ориентировочно описывается уравнением lnD* = 11,62/RT* + 17751 (R2 = 0,9194). С учётом принципа равенства размерностей коэффициент при RT* можно представить, как Q*, а свободный член – lnD**, т.е. окончательное уравнение бикомпенсации имеет вид
lnD* = Q*/RT* + lnD**
или более правильно [32]
ln(D*/D**) = Q*/RT* .
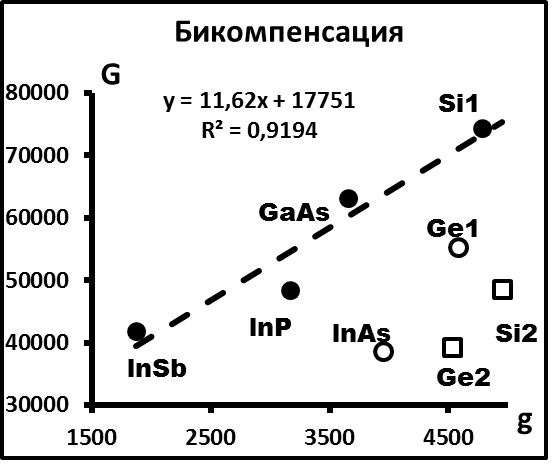
Рис.5. Диаграмма бикомпенсации в полупроводниках.
Положение прямых КУ в стёклах зависит от состава, и диаграммы описывают некоторые свойства уже самой матрицы. В искусственных стеклах c ростом Q катионы образуют последовательность:
Здесь минимальной энергией Q обладают элементы самой матрицы. Для матриц с двухвалентными диффундантами на первом месте стоят элементы, сумма ионных радиусов которых с радиусом диффунданта равна для обеих меток и обладает минимальными значениями, приближаясь к величинам расстояний между элементами и ионом кислорода. Прочие диффунданты следуют по возрастанию атомного веса или ионного радиуса.
КУ-2. Распределение одного и того же диффунданта в матрицах разного состава (рис.2.Б-1). Этот рисунок иллюстрирует то положение, что и в этом случае возможно появление, например, двух выборок, природа которых не изучена. Эти диаграммы отражают, видимо, свойства самих меток. В простейших системах положение прямых КУ определяется, в первую очередь, валентностью диффунданта. Если дан Y+1, то прямые КУ совпадают. Для ионов Y+2 прямые КУ уже разделяются.
Сводный перечень компенсационных уравнений приведен в табл.3. Он охватывает 509 КУ, или 53% всего количества уравнений. Попытки построения диаграмм бикомпенсации не дали положительных результатов. Даже использование выборок для одного элемента, например, кислорода, привело к образованию только «облачного» распределения.
|
№№ п.п.
|
Диф- фундат
|
Q= alnDo+ A;
|
R2
|
N
|
Матрица
|
|
|
a
|
A
|
|||||
|
1
|
C
|
2371,1
|
51960
|
0,963
|
5
|
ДЛ,КЛ,КЛ11С,КЛ1С,КВ[ГР](3&), КО,ОЛ
|
|
2
|
C
|
1508,8
|
42430
|
0,9912
|
6
|
Р,Mo, ẞ-Ti,α-Ti
|
|
3
|
C
|
1788,7
|
28034
|
0,9901
|
9
|
Fe(2,6Mo), Fe(0,9Cr),Fe(3,6Si),Fe(0,6Mo),
Fe(2,5Si),Fe(0,8Si),Fe(2,0Ni),Fe(0,6Ni),Fe(100)
|
|
4
|
O
|
2183,1
|
61329
|
0,9919
|
15
|
ЩБЗ(2&),Б,АД(2&),OP(98),МК,AЛ(97),АН(96),ФA,АН,ТЛT
|
|
5
|
O
|
2840,7
|
106866
|
0,9732
|
8
|
MgAl2O4,ОЛ(Со),OЛ(Fe)(4&),БЗТ,КВ[ГР], МТ
|
|
6
|
O
|
3855,4
|
41990
|
0,9997
|
4
|
ЩБЗ(2&), НФТ, АЛ(96)
|
|
7
|
O
|
3327,6
|
61057
|
0,9966
|
8
|
UO2[KP], α-Fe2O3,Sc2O3,Y2O3,Ho2O3,Er2O3,Tn2O3
|
|
8
|
O
|
9474,5
|
79671
|
0,9942
|
4
|
A12O3[РЭ], α-Cr2O3,UО2[KP],Lu2O3,
|
|
9
|
O
|
2262,1
|
46665
|
0,9878
|
10
|
ẞ-Ti(4&), α-Ti(5&),Ti
|
|
10
|
O
|
2905,4
|
38444
|
0,998
|
6
|
ẞ-Ti(5&),Nb
|
|
11
|
Na
|
2715,2
|
54642
|
0,9927
|
14
|
ЩП,АЛ(98)(4&),АЛ(100)(2&),АЛ(4&),OР,МИ,АД(86)
|
|
12
|
Na
|
1283
|
38428
|
0,9562
|
6
|
НФ(2&),АН,KС,СД,КР
|
|
13
|
Na
|
2895,8
|
31293
|
0,9633
|
13
|
В1,В2,В4,Г1(4&),Г2,Г3,Д1,Д2,Д3,Д4
|
|
14
|
K
|
2635,4
|
34672
|
0,9864
|
6
|
Д6,Д7,Д8,Д9,Г4
|
|
15
|
K
|
2129,4
|
69428
|
0,9998
|
4
|
ПРТ,БЗТ,ФНТ,РЛТ
|
|
16
|
Rb
|
2268,2
|
31535
|
0,9775
|
4
|
В1,В2,B3,B4
|
|
17
|
Rb
|
4859,5
|
57529
|
0,9934
|
6
|
OР(94)(2&),ФЛ,ОР(94),ОРс,АЛс,ЦШ
|
|
18
|
Li
|
2809,2
|
33680
|
0,9923
|
7
|
Pitch-stone,OР.ст,КВ[ГР],ЩБЗ,AHT,LiF[KP]
|
|
19
|
Li
|
8649,9
|
37297
|
0,9884
|
5
|
Pitch-stone,АНТ,АЛ.ст,БЗТ,GaSb[КР]
|
|
20
|
Cs
|
6678,2
|
53631
|
0,9809
|
7
|
AHT,МГМ,БЗТ,АНТ,Pitch-stone,пантелер.,ОБС
|
|
21
|
Cs
|
2653,4
|
31749
|
0,9883
|
4
|
В1,В2,B3,B4
|
|
22
|
Ca
|
2842,1
|
80258
|
0,978
|
8
|
CaFe2O4, α-Ca2SiO4,Ca3Si2O7, α-CaSiO3,b-CaSiO3,
CaO(поверх),CaO(объем),CaO
|
|
23
|
Sr
|
2855
|
48190
|
0,9812
|
5
|
ЩБЗ,АНТ(2&),БЗТ(2&)
|
|
24
|
Sr
|
6712,9
|
90425
|
0,9912
|
9
|
ЦШ,ДП#,OЛ(Mn),ФЛ,ОР(94)(2&),МИ(100),МИ,SrO
|
|
25
|
Sr
|
8069,4
|
65089
|
0,9996
|
3
|
ДП+,ОБС,БИ
|
|
26
|
Ba
|
3479,6
|
55581
|
0,9601
|
9
|
ЦШ,BaF2,АНД,ЩБЗ,ОБС,пантелер.,АНТ,BaO(2&)
|
|
27
|
Pb
|
2729,4
|
42600
|
0,7346
|
13
|
СФ(2&),АП(4&),МИ,ПП,АЛ(96),UO2[KP],ЦР(2&),МH(2&),
ГЛ[КР],Аg[КП]
|
|
28
|
Cr
|
2714,2
|
77536
|
0,9945
|
10
|
Cr(3&),CrO3(6&),a-Cr2O3
|
|
29
|
Co
|
2592,6
|
46356
|
0,9943
|
5
|
ШБЗ,Pitch-stone,БЗТ,АНТ(2&)
|
|
30
|
Fe
|
3890,3
|
55036
|
0,9789
|
7
|
ВAP,АНТ(2&),БЗТ(2&),ФНТ,Pitch-stone
|
|
31
|
Fe
|
1944,9
|
57107
|
0,9983
|
4
|
MgO(4&)
|
|
32
|
Fe
|
2475,2
|
55859
|
0,9725
|
4
|
СР[КР],Ti,Fe(2,0Ni)(2&),Fe(3&)
|
|
33
|
Fe
|
1253,7
|
24634
|
0,987
|
7
|
Бор5,Ti,Ge,Si,InSb
|
|
34
|
Sn
|
3331,6
|
59542
|
0,987
|
4
|
Ti, ẞ-Ti(2&),Ge
|
|
35
|
Si
|
2835,5
|
94665
|
0,9845
|
4
|
OЛ(Fe),ОЛ(Со)(2&),ОЛ(Zn)
|
|
36
|
Si
|
3039,6
|
64972
|
0,9885
|
4
|
ВAP,ВЗТ,ФНТ,РЛТ
|
|
37
|
Si
|
6126,1
|
60824
|
0,9863
|
4
|
Si(111)
|
|
38
|
Al
|
3054
|
58995
|
0,8993
|
10
|
P(КЦ),ОЛ,E, ẞ-Ti(3&), α-Ti,Ge,Si(2&)
|
|
39
|
Ti
|
2310,2
|
66822
|
0,9868
|
5
|
БЗТ,ФНТ,РЛТ,З, α-Ti,Ti
|
|
40
|
Zn
|
2752,7
|
47344
|
0,9756
|
9
|
СР[КР](3&),Si,AlSb[КР],GaSe(2&),GaAs,InAs
|
|
41
|
H
|
-632,97
|
5732
|
0,9818
|
7
|
КВ[ГР](3&),Mg-кордиер,Fe-кордиер,ЭП11С,ЭП1С,ЦЗ11C(2&),
ЦЗ1С,МУ11 С,МУ1 С
|
|
42
|
H
|
2856,6
|
24161
|
0,9618
|
12
|
ẞ-Ti(2&), α-Ti(5&),Ni(ГП)(3&),Mo, α-TiJ4, ẞ-TiJ4.
|
|
43
|
N
|
3256,9
|
61099
|
0,9926
|
10
|
СЛ,ФЛ, α-Ti(5&),TiN,БИ
|
|
44
|
P
|
7420,5
|
57262
|
0,9104
|
5
|
Ge,Si(2&),Р[КГ],Ti
|
|
45
|
He
|
2685,8
|
26629
|
0,9983
|
6
|
ОБС(2&),ПРТ,CИ,Ge
|
|
46
|
Ar
|
2554,6
|
57345
|
0,9779
|
14
|
ФЛ(2&),СЛ,ЛД(2&),КШ,OP(94),ПШ(2&),СН(75)(2&),
ОP,БЕ(2&),
|
|
47
|
Ar
|
810,7
|
33475
|
0,6882
|
13
|
ПШ,СИ,ПП,МИ(100),БИ(2&),KF[KР](2&),ЛЦ,KBr[KР],
KJ[KР],ФЛ,ГФ
|
|
48
|
Xe
|
6709,2
|
168347
|
0,9882
|
5
|
UО2[KP](4&),U3O8
|
|
49
|
Rn
|
2676
|
95528
|
0,9927
|
5
|
Fe2O3[KP],Al2O3[РЭ](2&),ThO2[РЭ],UO2[KP]
|
|
50
|
Cl
|
1148,5
|
30416
|
0,8993
|
4
|
CsCl[KP],AgCl[КP](3&)
|
|
51
|
Mo
|
6058,1
|
106075
|
0,9412
|
12
|
Mоp,Mo[КЦ](5&),Mo(поликрист)(6&)
|
|
52
|
Mo
|
17141
|
87054
|
0,9549
|
6
|
W(25Mo),W(65Mo),W(75Mo),W(80Mo),W(85Mo),W(99,9Mo)
|
|
53
|
Mo
|
5881,5
|
72803
|
0,9963
|
5
|
W(15Mo),W(20Mo),W(25Mo),W(35Mo),W(50Mo)
|
|
54
|
W
|
9399,4
|
119821
|
0,9706
|
6
|
|
|
55
|
W
|
4454,1
|
113084
|
0,9724
|
4
|
|
|
56
|
W
|
59156
|
159092
|
0,9134
|
5
|
W(поликр.),
|
|
57
|
W
|
61317
|
-67628
|
0,9797
|
6
|
W(монокр.)(8&)
|
|
58
|
W
|
-59156
|
159092
|
0,9134
|
6
|
W(50Mo),W(65Mo),W(75Mo),W(80Mo),W(85Mo),W(99,9Mo)
|
|
59
|
W
|
7464,5
|
70701
|
0,9973
|
4
|
W(15Mo),W(20Mo),W(25Mo),W(35Mo),W(50Mo)
|
|
60
|
Nb
|
3319,9
|
97679
|
0,8677
|
10
|
Nb(поликрист)(6&),Nb[КР](4&)
|
|
61
|
Nb
|
3346,5
|
60410
|
0,9957
|
9
|
Zr[КР],Zr[ГР],Zr(2,5Nb),Zr(5,0Nb)(2&),Zr(10Nb),
Zr(15Nb),Zr(7,5Nb),Ti
|
|
62
|
Zr
|
3114,3
|
57913
|
0,9866
|
16
|
Zr(1,0Nb),Zr(1,5Sn),Zr(2,0Nb),Zr(2,5Nb),
Zr(5,0Nb)(2&),Zr(7,3Nb),Zr(7,5Nb),Zr(10Nb)(2&),
Zr(20Nb),Zr(10Mo),Zr(15Mo),Zr(100),Zr,Zr-2
|
|
63
|
U
|
2477
|
108064
|
0,9953
|
4
|
UO2[КР],Nb[КЦ],Ta[КЦ],Mo[КЦ]
|
|
64
|
U
|
2962,5
|
54653
|
0,9771
|
6
|
ẞ-Zr[КР](2&), ẞ-Ti[КР],Zr[КР](3&)
|
|
65
|
Be
|
3966,2
|
71260
|
0,9693
|
4
|
BeO[КР],Be[МУ],GaAs,Ge
|
|
66
|
Ga
|
3321,2
|
75973
|
0,9969
|
6
|
GaAs,GaAs[КР],Si(2&),Si(P),Si(B)
|
|
67
|
In
|
633,94
|
81472
|
0,9813
|
5
|
InР,InP[КР],InAs,InSb[КР],Si
|
|
68
|
Cu
|
1875,5
|
27975
|
0,9331
|
5
|
Ge(2&),InР,InSb,Si
|
|
69
|
Cu
|
2586,7
|
22475
|
0,9976
|
5
|
Ge,Бор4,InAs,AlSb[КР],Si
|
|
70
|
Ge
|
4064,7
|
69062
|
0,9357
|
6
|
Ge,Ge[КР],GaAs,InSb,Si(2&)
|
|
71
|
Bi
|
5225,6
|
61475
|
0,9488
|
4
|
Ge,Вi1c[РЭ],Si(2&)
|
|
72
|
Cd
|
845,72
|
29385
|
0,9721
|
4
|
InР,GaAs,InSb,GaSb,Si
|
|
73
|
Sb
|
10179
|
66583
|
0,9663
|
5
|
Ge,Si(2&),GaSb,InSb
|
|
74
|
As
|
3469
|
60207
|
9,927
|
8
|
Ge,Si(3&),GaAs(3&),InAs
|
Примечание к таблице 3:
|
11С -параллельно оси С; 1С-перпендикулярно оси С.
|
||||||
|
Вида диффузии: МУ-межузельная, ДЦ- диссоциативная; пов -поверхностная,
объем- объемная.
|
||||||
|
КВ[ГР]-тип решетки матрицы: кубическая- КЦ-центрированная; КП-плотная, КР-кубическая; КГ-гранецентрированная. Гексагональная- ГП-плотная; ГР-гексагональная; Ромбические: РЭ-ром6оэдрическая; РР-ромбическая. ТР- тетрагональная.
|
||||||
|
Тип примеси в полупроводниках: акц-акцептор, дон- донор, нтр-нейтральный.
|
||||||
|
Минералы: АД-адуляр, АЛ-альбит, АН-анортит, АП-апатит, АЦ-анальцим, БЕ-берилл, БИ- биотит; ГК-глауконит, ГЛ-галенит, ГС-гроссуляр, ГФ-глаукофан, ДЛ-доломит, ДП-диопсид; ЖД- жадеит, ИЛ-иллит, КА-каолин, КВ-кварц, КА-кальцит, КO-кордиерит, КР-криолит, КС- кальсилит, КШ-калиевый полевой шпат, ЛД-лепидолит, ЛР-ларнит, ЛЦ-лейцит, МИ-микроклин, МН-монацит, МУ-мусковит, НФ-нефелин, ОЛ-оливин, ОП-ортопироксен, ПГ-полигалит, ПП-плагиоклаз-пертит, ПР-пироп, ПШ-полевой шпат, СД-содалит, СИ-сильвин, СЛ-слюда, СН-санидин, СР-сфалерит, СФ-сфен, ФЛ-флогопит, ЦЗ- цоизит, ЦР-циркон, ЦШ-цеолит- шабазит, ЩЛ- щелочной полевой шпат, с-стекло, ЭП- эпидот.
Для АЛ в скобках-доля молекулы АЛ. Для калиевых полевых шпатов - доля молекулы ортоклаза. ОЛ(Fe)-фаялит; Fe2SiO4; ОЛ(Mg)-форстерит Mg2SiO4; ОЛ(Со)-Cо2SiO4, ОЛ(Zn)- виллемит Zп2SiO4.
|
||||||
|
МРР- мрамор, МТТ- метеорит, НФТ-нефелинит, ОБС- обсидиан, ПРТ-перлит, РАТ-риолит, ТАТ-толеит, ФНТ-фонолит, ЩБЗ-щелочной базальт, р - расплав.
|
||||||
|
(3&) - Данное соединение встречено 3 раза и т.д. (2,0Ni) – количество примеси в соединении.
|
||||||
|
Стёкла:
|
||||||
|
А-MgОхAl2О3 (MgAl2O4);
|
Г1-Na2Ox2SiO2;
|
Д5-K2OxCaOx4SiO2;
|
||||
|
А1-MgOx1,2Аl2О3;
|
Г2-Na2ОxLi2Оx4SiO2;
|
Д6-K2OxLi2Ox4SiO2;
|
||||
|
Б-CaA12SiО6;
|
ГЗ-Nа2OxK2Оx4SiO2;
|
Д7-K2OxВаOx4SiO2;
|
||||
|
В1-Na2Ox3SiO2;
|
Д1-Na2ОxCaОx4SiO2;
|
Д8-K2OxSrOx4SiO2;
|
||||
|
В2-K2OxSiO2;
|
Д2-Na2ОxBaОx4SiO2;
|
Д9-K2OxMgOx4SiO2;
|
||||
|
ВЗ-Сs2Ox3SiO2;
|
Д3-Na2ОxSrОx4SiO2;
|
E-Сa3Si2О7;
|
||||
|
B4-Rb2Ox3SiO2;
|
Д4-Na2OxMgOx4SiO2;
|
З-Fe2TiO4.
|
||||
|
|
Na2O
|
B2O3
|
SiO2
|
CaO
|
Al2O3
|
|
|
Бор1
|
25
|
49
|
26
|
|
|
|
|
Бор2
|
8,6
|
4,28
|
20
|
28,6
|
14,3
|
|
|
Бор3
|
22,4
|
44,3
|
22,5
|
4,3
|
6,5
|
|
|
Бор4
|
22,4
|
44,3
|
22,5
|
4,3
|
6,5
|
|
|
Бор5
|
32
|
31
|
37
|
|
|
|
|
Бор5
|
32
|
31
|
37
|
|
|
|
|
Бор6
|
22,4
|
44,3
|
37
|
|
|
|
|
Бор7
|
32
|
31
|
37
|
|
|
|
|
Бор8
|
22,4
|
44,3
|
22,5
|
4,3
|
6,5
|
|
Существующие интерпретации КУ касаются только КУ-2 (теория Верта-Зинера- Ле Клера; Кузнецов,1979 [8]; Малкин и др.,1961; Магомедов, 1972 [10]; и др.). Величину Do часто связывают с внутренним строением кристаллической решетки; так по Верту – Зинеру - Ле Клеру Do = Van, (a- постоянная решетки, n- частота колебаний атома – метки около его положения равновесия, V- геометрический фактор). По Динесу (G.J. Dines, 1950) Do= knd2exp(E/RTпл) (k= const, n- дебаевская частота, d- межатомное расстояние; Тпл- температура плавления). Пределы изменения Do пытался оценить В.М. Катлинский (1984).
Наша попытка интерпретации КУ базируется на представлении уравнений диффузии в качестве уравнения прямой, проходящей через точку, являющейся эталонной. Если последняя является общей нескольких УД, то образуется КУ, преобразуемое в уравнение Q=RT*ln(Do/Dо*), а T* и Dо*, описывающие свойства матрицы, являются координатами точки кроссовера. Далее возможны варианты:
- согласно эмпирическому равенству Диннеса (1950) [8] можно положить, что Т*=Тпл, а D* = koωa2, где ω -частота колебания диффундирующего атома около положения равновесия, a2 - постоянная решетки (межатомное расстояние), k=const. Оказалось, что для расплавов T*> Tпл, для твердых тел (кристаллов) T*< Tпл, приближаясь к Т их образования [13, 14, 16] в природных условиях (например, для альбита Т*=421оС, калишпата- 507, флогопита -483, сфалерита- 624оС). Вместе с этим паpаметp Do зависит от Т, что не согласуется с постоянством Do. Кроме того, это выражение предполагает равенство величины ω для всех элементов, участвующих в процессе, чего не может быть.
-Если Do=D*, то Q=Q*=0 и ей соответствует критическое значение Dкр*. Для названных минералов значения lgDкр*= -15,10 (альбит); -14,36 (калишпат); -16,79 (флогопит) и -12,04(сфалерит) близки коэффициентам диффузии воды в расплаве альбита при Т= 1100-1400оС (Хитаpов и дp.,1975).
Взаимное диффузионное перемещение двух частиц описывается коэффициентом взаимной диффузии, свойства которого во многом аналогичны свойствам коэффициента самодиффузии. Однако, возможен и другой путь описания взаимодействия этих частиц, который в конечном счете ведет к разделению этих частиц. Последнее явление так называемого диффузионного фракционирования чаще всего используется при описании изотопных систем и на схеме отражено в верхней ее части.
Применительно к природным процессам этот вопрос впервые рассмотрел, видимо, W.Daansgaard [23]; в своих исследованиях этих вопросов касались M.K. Stewart [30], J.Hoefs [26], W. F.Giggenbach [25] и др. Диффузионную модель использовали также O.Mutsubaya, H.Sakai et al (1979 [27]). Для описания испарения водной капли в сухой воздух они использовали выражение α = αp (D/D')n, однако, четкого смысла в параметр n они не вкладывали. A.A.Verbeck et al [31] использовал эти представления при описании миграции изотопов 39К и 41К в зоне контактового метаморфизма, применив понятие о теоретической тарелке. Из соотечественников этой проблемы касались А.М. Зякун, А.Д. Бондарь (1980, 1987 [4]). Для описания условий фракционирования изотопов углерода при миграции СO2 и СН4 они применили понятия о стационарной (n= 0,5) и нестационарной (n=1) диффузиях. Однако, четких критериев для их выделения предложено не было, так же как и не предлагались вообще способы определения самого факта проявления диффузии.
α = αдn × αт ,
близкое выражение использовали D. Ehhalt [24], W.F. Giggenbach [25], причём выполняется уравнение (1)
δY = sδX + A, (1)
а величина углового коэффициента в (1) найдется из (2):
s=(lnα(Y)+nlnαд (Y))/(lnα(X)+ mlnαд (X)), (2)
в котором n и m -числа теоретических тарелок при разделении изотопов элементов Х и Y.
Таким образом, при проведении исследований по измеренным значениям δХ и δY строятся диаграммы их совместного поведения в изотермических условиях, с которых снимаются величины s. Далее формируется банк данных уравнений фракционирования и показателей диффузионного разделения (или коэффициентов диффузии изотопных разностей). По этим данным составляются ИГТ в виде отношений (2) и рассчитывается Тиз, сопоставляемая с измеренной To образования М. В случае расхождения их в (2) подставляются значения s и подбором n (или m) осуществляется согласование Тиз=То. Полученное n(m) является решением задачи.
Более сложное положение сложилось с базами данных со значениями αд и D*. Это связано с тем, что эксперименты по определению параметров уравнения Аррениуса касались ограниченного круга минералов и газовых смесей и только части компонентов. Например, имеются определения для 18О, 13С и отсутствуют такие же определения для изотопов 16О и 12С. Поэтому в большинстве случаев величина αд определялась из равенства αд= √(М/М*), где М и М* -молекулярные веса лёгкой и тяжёлой изотопных разностей.
Ниже рассмотрены несколько примеров анализа влияния диффузии на изотопный состав геологических объектов.
Изучение изотопного состава О и Н природных (поверхностных, подземных, атмосферных,) вод (ПрВ) способствует анализу условий их формирования. Знание этих проблем необходимо прежде всего в связи с расширяющимся экологическим загрязнением ПрВ, т.е. ухудшением свойств ПрВ за счет поступления в них различных компонентов. Составной частью изучения ПрВ является анализ механизмов формирования воды и ее источников. Последняя решается на основе изучения изотопного состава О и Н воды. К недостаткам этого подхода относится частое игнорирование температуры (T), минерализации (M), диффузии изотопных компонентов, состава (C) равновесного воде природного соединения, хотя их влияние отмечается во многих работах.
Вывод новых типов изотопных геотермометров [11, 12] позволил по-иному взглянуть на особенности формирования изотопного состава природных вод. Согласно [11, 12] у прямой (3), построенной по пробам воды, отобранным
dD= sd18O + A, (3)
в изотермических условиях, угловой коэффициент s зависит от Т и определяется равенством (4), где aхт и ayт -показатели термодинамического фракционирования изотопов Н и О между водой и изотопно-равновесным ей
s=(ln ayт (*H2O- Cy))/(lnαхт (H2O*- Cx))=fy(T)/fx(T), (4)
соединением соответственно Сн и Со; (*) отмечает изотопно-обменивающийся элемент; fy(T) и fx(T)- их температурные функции. Компоненты (4) отражают существующее термодинамическое изотопное равновесие (ТИР). В случае ТИР и отсутствия процессов, воздействующих на величину aт, выполняется равенство Тизм=Тиз (параметры: изм- измеренные, из-изотопные). При их наличии, например, диффузии, это равенство нарушается, что служит основой для установления влияния этого фактора. Далее d18O = dO, изотопный состав dO и dD выражается в единицах SMOW.
Природные пути движения (миграции) водных потоков- аналоги фильтрационных колонн [4]. Тогда отрезок пути, при прохождении которого под влиянием диффузии произойдет разделение изотопов на величину aд, называется теоретической тарелкой; общее разделение равно αдn, где n- число теоретических тарелок, характеризующих глубину диффузионного фракционирования [13]. В общем случае αд = (D1/D2), Di- коэффициенты диффузии легкой и тяжелой изотопных разностей. При совместном действии T и диффузии общее разделение изотопов опишется равенством (5) [13, 26]:
α= αт х αдn. (5)
Комбинация (5) и (4) создает окончательное значение углового коэффициента (6) для изотермы (5):
s = [lnαнт(*Н2О – Сн) + mlnαнд]/[ln aот(Н2О* - Со) + nlnαод] (6)
При установлении роли диффузии используются уравнения разделения изотопов (7) и (8) в системе жидкость (ж)- пар (п):
Значения αд в системе жидкость (ж)-пар(п) имеют значения: αдн(H2Oж-H2Oп) = 1,009, αдо(H2Oж-H2Oп) = 1,016. Тогда уравнение для определения величин n и m имеет вид (9):
(Tизм)2= (2,6-0,28s)106/[(24,3+9n) - (1,8+15,9m)s]. (9)
Как правило, m= 0, тогда (10)
n= 0,2s + 106[(2,6 -0,28s)/9(Tизм)2 ]- 2,7. (10)
2.При наличии большого количества выборок, описываемых уравнением (1), можно рассмотреть зависимость вида (11), в которой параметры A и s являются уже переменными.
A = ks + D*, (11)
Это уравнение называется компенсационным [16]. Оно описывает состав воды k=-d18O и D* =dD, характеризующий общую для выборок примесную компоненту из источника более глубокого уровня.
Имеющиеся данные позволяют наметить схему формирования взглядов на роль диффузии при магматическом и метаморфическом МО [15]. Обработка изотопных составов этих минералов проводилась по описанной выше схеме. В изотермических условиях происходит диффузионное разделение изотопов с показателем фракционирования αд=D/Dт= √Мт/М (D и Dт -коэффициенты диффузии, М и Мт- молекулярные веса легкой и тяжелой компонент). Представления о "теоретической тарелке" помогают оценить глубину этого разделения с помощью показателя n в равенстве α= αдn.
Исследования показали, что явления диффузии широко распространены в природе. В заведомо магматических образованиях кислого состава и карбонатитах эти явления пока не установлены. Однако, они выявлены при образовании минералов, содержащих в решётке воду, например, мусковитов, биотитов, роговых обманок и пр. метаморфических пород широкого класса. Для компоненты HDO в мусковитах аплитов, сланцев и гранито - гнейсов n= 0-1,0; в биотитах аляскитов, гранодиоритов, сланцев, гнейсов- 0-0,65; в роговых обманках гранодиоритов n=1,5 [15].
Кроме того, она проявлена при формировании высокотемпературных кальцитов скарнов и мраморов (табл.1). Здесь диффундантами является *H2O, *CH4, *CO2, CO2*.
Среди карбонатных образований диффузия сопровождает формирование широкого круга пород как органогенной, так и неорганогенной природы (табл.1) (кальциты экзогенные, гидротермальные, мраморов, скарнов, кальцифиров). Основными диффундантами являются *H2O, *CH4, *CO2, CO2*. Величина n (глубина диффузионного фракционирования) изменяется в пределах 0,03-1,5 (*H2O); 0,25-2 (*CH4); 0,05-3 (*CO2) (табл. 4) .
|
Cемейство, вид
породы
|
Место отбора
|
Воз-раст
|
Равновесные соединения
|
Источник
|
|
|
По *С
|
По *H
|
||||
|
Cellana sp.
|
Антарктида
|
Q
|
CH4(1/4)
|
H2O
|
Dorman P., 1968
|
|
Naccella deles.
|
Антарктида
|
Q
|
CH4
|
H2O(1/30)
|
Dorman P., 1968
|
|
Mulinia sp.
|
USA
|
Q
|
CH4
|
H2O(1/20)
|
Keith M.L., 1965
|
|
Eolianites sp.
|
USA
|
Q
|
CH4
|
H2O(1/9)
|
Dorman P., 1968
|
|
Криноидеи
|
|
Q
|
CH4
|
H2O(0,7)
|
Webek J.N.,1968
|
|
Classostrea sp.
|
USA
|
Q
|
CH4
|
H2O(0,7)
|
Keith M.L., 1965
|
|
Строматолиты
|
Гималаи
|
|
CO2
|
H2O(0,7)
|
Pondey G.C,1970
|
|
Sorites marginal
|
Атлант.океан
|
Q
|
CO2(2)
|
H2O
|
Weber J.N., 1968
|
|
Dendrophyllia sp
|
Тихий океан
|
P
|
CO2(2)
|
H2O
|
Veizer J., 1976
|
|
Белемниты
|
Альпы
|
J
|
CO2(1/4)
|
H2O
|
Webek J.N.,1968
|
|
Astropecten sp.
|
Сирия и др.
|
Q
|
CO2(1/3)
|
H2O
|
Keith M.L., 1965
|
|
Mulinia sp.
|
USA
|
Q
|
CO2(0,7)
|
H2O
|
Keigwin L., 1974
|
|
Orbulina sp.
|
Тихий океан
|
N
|
CH2O
|
CH2O
|
Keigwin L., 1974
|
|
Uvigerina sp
|
Тихий океан
|
Q
|
CH2O
|
CH2O
|
Veizer J., 1976
|
|
Белемниты
|
Альпы
|
J
|
CH2O
|
CH2O
|
Голышев С.1981
|
|
Строматолиты
|
В. Сибирь
|
Cm
|
CH2O
|
CH2O
|
Lloyd M.R, 1964
|
|
Известняк
|
Германия
|
Q4
|
CH4(2,0)
|
H2O
|
Degens E.T.,1964
|
|
Известняк м.з.
|
Приморье
|
K
|
CO2(0,6)
|
H2O
|
Киселев В.И., 1988
|
|
Известняк
|
Англия
|
J
|
CO2(1/5)
|
H2O
|
Tan F.C., 1971
|
|
Карбонат диаген.
|
Марок. впад.
|
N
|
CO2(1,5)
|
H2O
|
Галимов Э.,1982
|
|
Ирландия
|
K
|
CO2
|
H2O(1/6)
|
Boast A.M., 1981
|
|
|
Известняк
|
Донбасс
|
С
|
CO2
|
CO2
|
Курило М.В, 1984
|
|
Известняк
|
Оз. Ханка
|
Cm
|
CO2
|
CO2
|
Киселев В.И.,1988
|
|
Конкреция
|
Англия
|
|
CH4
|
H2O(1/3)
|
Coleman M.,1981
|
|
Конкреция
|
Пай- Хой
|
|
CO2
|
CO2
|
Юдович Я., 1984
|
|
Сталактит
|
Италия
|
|
CH4(1,5)
|
H2O
|
Dudas M.J., 1968
|
|
Сталактит
|
Италия
|
|
CH4
|
H2O(1/2)
|
Fornaca- Rinaldi G., 1968
|
|
Травертин
|
Йеллоуст. п.
|
|
CO2(2)
|
H2O
|
Friedman J.,1970
|
|
Цемент конглом.
|
Калифорния
|
|
CH4
|
H2O(1/30)
|
Barnes J., 1971
|
|
Примечания: в скобках – глубина диффузионного фракционирования; сокращения: п.- парк, м.- море, м.з.- мелкозернистый.
|
|||||
Таким образом, в результате проведённых работ была отработана методика учёта и изучений такого явления, как диффузия изотопов в природных образованиях. Иследования показали, что явления диффузии достаточно широко распространены в природе. В заведомо магматических образованиях кислого состава и карбонатитах эти явления не проявлены. Однако, они выявлены при образовании слюд и амфиболов метаморфических пород широкого класса. Здесь диффундантом является *H2O. Среди карбонатов диффузия сопровождает формирование широкого круга пород как органогенной, так и неорганогенной природы (кальциты экзогенные, гидротермальные, мраморов, скарнов, кальцифиров). Основными диффундантами являются газы *H2O, *CH4, *CO2, CO2*.
Анализ показал, что результаты теоретических исследований не применимы для решения геологических задач. Кроме того не определён круг геологических задач, которые можно решать с помощью диффузионных методов. Эти исследования так и не выявили механизм связи между Q и lnDo.
Литература.
32. Макаров В.П. Абсолютная аддитивность. /Сб. Владимир Макаров. Механизмы выделение минералов. Уравнения компенсации. Задачи об источниках вещества. М.: Lambert Academic Pablishing. 2019. С 103 - 113. ISBN: 978-620-0-26191-5.
33. Макаров В.П. Влияние диффузии на распределение изотопов в процессах природного минералообразования. /Изотопные геотермометры. Решение задач о смешении и источниках вещества. М: Lambert Academic Publishing. 2019. C.94 - 114. ISBN: 978-613-9-46137-0.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии