Гелий. Вопросы геохимии благородных газов
ГЕЛИЙ. ВОПРОСЫ ГЕОХИМИИ БЛАГОРОДНЫХ ГАЗОВ.
В.П.Макаров
Гелий - это один из триады (аргон [36, 39], гелий [1, 2, 16, 38] и неон [37, 40]) благородных газов, широко используемых для определения абсолютного возраста геологических образований. Существует даже специально разработанная методика определения возраст с использованием гелия [4]. Пример одного из уравнений для определения возраста имеет вид (формула Холмса):
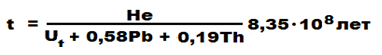
Основные свойства гелия изложены в работах [1, 2]. В работе [2] кратко описаны основные приёмы определения газа в пробе, в которых газы находились уже в выделенном состоянии. Однако способы выделения газа из проб твёрдого состава не приведены. В настоящее время основным является пирохимический метод, т.е. выделение газа при высоких температурах (например, до 1150-1200оС [28]).
Исследования показали, что гелий в разных количествах присутствует во многих минералах (прежде всего радиоактивных – тюямунит, уранинит, монацит, торианит и др. [3, 5], а также бериллиевые, литиевые, борные минералы [5], рутил, касситерит, гранат, ильменит [7], сподумен и берилл [8], ортопироксен, плагиоклаз, клинопироксен, оливин, амфибол, хромит, бронзит [35], алмазы и пр.) и в метеоритах [9, 10, 11 и др.]. Но в подавляющем большинстве случаев изучаются значения содержаний изотопов и их отношения. В ряде случаев имеются экспериментальные определения динамики изменения поведения этих параметров с изменением температуры. Ниже приведены результаты анализа известных исследований по этой теме. Далее на всех рисунках и в таблицах объёмные концентрации изотопов выражаются в единицах 10-8 см3/г (породы).
МИНЕРАЛЫ.
Сподумен. Экспериментальный прогрев единичного образца описан в работе [8]. На рис. 1 приведён результат этого прогрева. Согласно этим данным, поведение изотопных отношений описывается уравнением
ln(4V/3V) = 4,8958(1000/ToK)2 – 13,738(1000/ToK) + 21,424 (R2 = 0,8598)
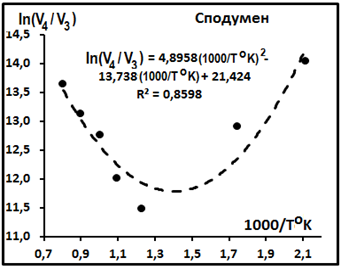
Рис. 1. Характер распределений изотопных отношений гелия в сподумене в зависимости от изменения температуры.
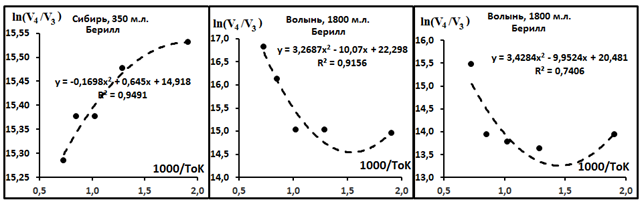
Рис. 2. Характер распределений изотопных отношений гелия в берилле в зависимости от изменения температуры.
Берилл. Там же приведены результаты экспериментальных исследований трёх образцов берилла разного возраста и мест отбора. Здесь также получены полиномиальные распределения отношений изотопов, но уже появляется разделение на два типа: с положительным знаком при первом типе распределений как в сподумене (бериллы Волыни) и с отрицательным знаком (берилл Сибири), говоря о возможном отличии механизмов фракционирования изотопов неона.
МЕТЕОРИТЫ.
Рассмотрены работы с результатами пироисследований метеоритов: Fayetteville (тип H), Kapoeta (Hov), Nogoya (Carbonoceous meteorite – CM-2), Renazzo (CM-2, 3) [9, 10, 11].
Изотопы 4He – 3He. Типичный пример распределений показан на рис.3.
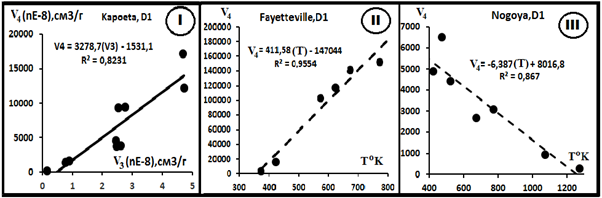
Рис.3. Характер зависимости между изотопами гелия.
Он показывает, что в пробах может быть несколько фракций, что, возможно, говорит о разных формах нахождения в них изотопов гелия. В табл.1 приведены сводные данные по связи изотопов гелия между собой. Таким образом в некоторых пробах между изотопами
Таблица 1. Уравнения связи между изотопами гелия.
|
Метеорит
|
Образец
|
Уравнения связи
|
R²
|
|
|
Kapoeta
|
D1
|
(4V) = 3278,7(3V) - 1531,4
|
0,8231
|
1
|
|
Kapoeta
|
D3
|
(4V) = 4048,7(3V) - 9325,2
|
0,9825
|
1
|
|
Kapoeta
|
D4
|
(4V) = 3884,6(3V) - 6883,1
|
0,9952
|
1
|
|
Fayetteville-2.
|
D1.
|
(4V) = 2413,7(3V) + 2277,9
|
0,9973
|
1
|
|
Kapoeta
|
D2
|
(4V) = 3595,9(3V) - 1667,9
|
0,9838
|
2
|
|
Fayetteville-2.
|
D2.
|
(4V) = 1849,8(3V) +251,47
|
0,9974
|
2
|
|
Renazzo
|
D2.
|
(4V) = 312,99(3V) + 16,257
|
0,9174
|
2
|
|
Nogoya
|
D2.
|
(4V) = 2573,6(3V) + 765,96
|
0,93
|
2
|
|
Nogoya
|
D1.
|
(4V) = 2985,1(3V) - 84,104
|
0,9909
|
2
|
4V=A(3V) + B. (1)
Здесь 3V = V(3He) и 4V = V(4He) – объёмы выделенных порций газов соответственно 3H и 4He. Это уравнение описывает температурную прямую, т.е. прямую, каждой точке которой соответствует своя, отличная от других температура. Это означает, что содержания изотопов гелия в пробах изменяется синхронно. Однако смысл параметров A и B не известен. На рис.4 приведена компенсационная диаграмма по данным табл.1. Согласно этим данным, всё множество уравнений связи разбивается на два семейства, которые в табл. 1 отмечены цифрами 1 и 2. Семейство 1 описывается уравнением B1 = -6,6372 (A) + 18507.
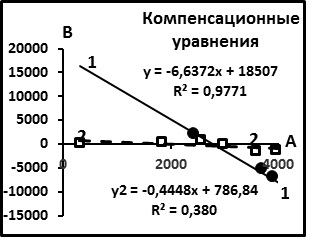
Рис.4. Компенсационные диаграммы по параметрам уравнений связи
Согласно [12] это свидетельствует о том, что гелий из проб этого семейства, принадлежа разным источникам, имеют один и тот же исходный состав газа с параметрами 4Vо = 18507•10-8 см3/г и 3Vо = 6,6372•10-8 см3/г. Пробы семейства 2 располагаются вдоль оси абсцисс. Его уравнение имеет вид B2 = -0,4448(A) + 786,84.
На рис.5 отражена зависимость концентраций изотопов гелия от Т. Выделяются несколько видов распределений концентраций изотопов, отражённых на этом рис.5:
В некоторых породах установлены по две фракции гелия. Пример этого приведён на рис.6 для метеорита Fayatteville.
Сопоставление с зависимостью между изотопами показывает, что зависимость вида рис.5-I и рис.5-II характерна для метеорита Fayetteville-2, В табл.2 приведены сводные данные по результатам изучения температурной зависимости изотопов He. Были изучены метеориты Fayatteville, проба D1 [9], Kapoeta, проба D3 [9] и Nogoya, проба D1 [10].
В этой таблице пробы, выделенные жирным шрифтом и подчёркнутые, относятся ко второму типу распределения. Пробы, выделенные
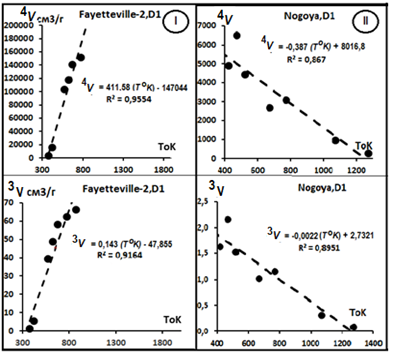
Рис.5. Температурная зависимость концентраций изотопов гелия.
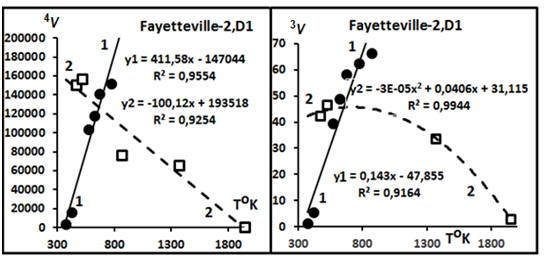
Рис.6. Пример двух фракций гелия в метеорите.
только жирным шрифтом, относятся к первому типу. Остальные пробы - к третьему типу. По материалам табл.2 построены компенсационные диаграммы вида
Таблица 2. Температурная зависимость распределений изотопов гелия.
|
Метеорит
|
Проба
|
Уравнение
|
R²
|
|
Fayetteville-2.
|
D1.
|
3V= 0,0726(ToK) + 4,6252
|
0,8281
|
|
Fayetteville-2.
|
D2.
|
3V= 0,0276(ToK) - 5,5702
|
0,8615
|
|
Nogoya
|
D1.
|
3V= -0,0022(ToK) + 2,732
|
0,8951
|
|
Nogoya
|
D2.
|
3V= -0,0018(ToK) + 2,516
|
0,9846
|
|
Fayetteville-2
|
D1
|
3V= 0,143(ToK) - 47,855
|
0,9164
|
|
Kapoeta
|
D1
|
3V= -0,0048(ToK) + 5,889
|
0,7464
|
|
Kapoeta
|
D3
|
3V= -0,0663(ToK) + 44,822
|
0,9369
|
|
Kapoeta
|
D4
|
3V= -0,053(ToK) + 35,034
|
0,9376
|
|
Fayetteville-2.
|
D1.
|
4V= 411,58(ToK) - 147044
|
0,9554
|
|
Fayetteville-2.
|
D2.
|
4V= 8,84(ToK) - 25108
|
0,8461
|
|
Nogoya
|
D1.
|
4V= -6,387(ToK) + 8017
|
0,867
|
|
Nogoya
|
D2.
|
4V= -3,617(ToK) + 6571
|
0,9481
|
|
Fayetteville-2
|
D1
|
4V= -100,12(ToK) + 193518
|
0,9254
|
|
Kapoeta
|
D3
|
4V= -268,06(ToK) + 171867
|
0,9169
|
|
Kapoeta
|
D4
|
4V= -241,32(ToK) + 150897
|
0,7774
|
B =γA + Γ, представленные на рис.7. эти материалы свидетельствуют о том, что
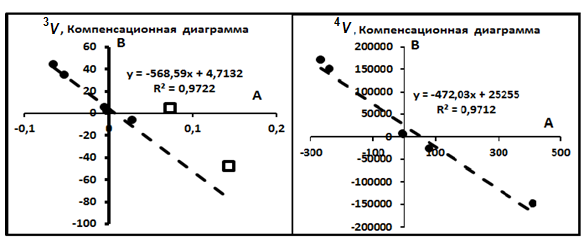
Рис.7. Компенсационные диаграммы для температурных прямых.
изотопы изученных метеоритов образуют семейства, в основе которого лежит наличие единого источника. По этим данным для 3He имеем Tо ≈ 569oK, 3Vo =4,71 cm3/г; для 4He – Tо ≈ 472oK, 4Vo = 25255 cm3/г.
Рассмотрим теперь изотермическое распределение изотопов гелия. В табл. 3 приведён пример построения соответствующей выборки.
Таблица 3. Параметры изотермичеких распределений изотопов гелия.
|
Meteorites
|
Образец
|
ТоС
|
1000/ToK
|
He n•10-8см3/г
|
|
|
3V
|
4V
|
||||
|
Fayetteville
|
D2
|
100
|
2,681
|
1,029
|
2514
|
|
Nogoya
|
D2
|
100
|
2,681
|
0,272
|
678
|
|
Kapoeta
|
D2
|
100
|
2,681
|
1,71
|
5840
|
|
Kapoeta
|
D1
|
100
|
2,681
|
0,34
|
1045
|
|
Fayetteville
|
D1
|
100
|
2,681
|
1,34
|
3180
|
|
ayetteville
|
D2
|
300
|
1,745
|
8,41
|
16280
|
|
Renazzo
|
D2
|
300
|
1,745
|
0,75
|
150
|
|
Nogoya
|
D2
|
300
|
1,745
|
2
|
5680
|
|
Kapoeta
|
D2
|
300
|
1,745
|
2,58
|
5844
|
|
Kapoeta
|
D1
|
300
|
1,745
|
2,460
|
4530
|
|
Fayetteville
|
D1
|
300
|
1,745
|
39,2
|
103300
|
|
Nogoya
|
D1
|
300
|
1,745
|
2,87
|
8350
|
|
Fayetteville
|
D2
|
500
|
1,294
|
16,18
|
30900
|
|
Nogoya
|
D2
|
500
|
1,294
|
1,25
|
3480
|
|
Kapoeta
|
D2
|
500
|
1,294
|
1,24
|
5847
|
|
Kapoeta
|
D1
|
500
|
1,294
|
2,6100
|
3900
|
|
Fayetteville
|
D1
|
500
|
1,294
|
62,4
|
151800
|
|
Nogoya
|
D1
|
500
|
1,294
|
1,16
|
3090
|
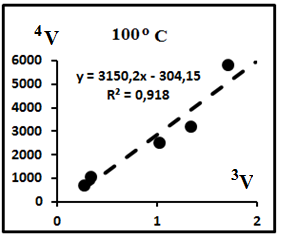
Рис. 8. Пример изотермического распределения изотопов.
В табл.4 приведены окончательные уравнения изотермических распределений изотопов гелия,
Таблица 4. Уравнения изотермических распределений изотопов гелия.
|
ToC
|
Уравнения
|
R²
|
|
100
|
4V = 3150,2(3V) - 304,15
|
0,918
|
|
200
|
4V = 3594,8(3V) - 3633,4
|
0,992
|
|
300
|
4V = 2655,6(3V) - 1515,2
|
0,996
|
|
400
|
4V = 2385,7(3V) - 792, 23
|
0,987
|
|
500
|
4V = 2421,0(3V) - 1063,5
|
0,996
|
|
1000
|
4V = 1390,3(3V) + 444,12
|
0,995
|
они имеют вид 4V = A(3V) + B, а на рис. 9.А – график зависимости угловых коэффициентов A (чёрные точки) от температуры. Морфологически уравнение изотермы близко температурному уравнению (1). Для их отличия уравнение изотермы будем изображать через выражение
4VT=AT(3V) + BT. (2)
Оно читается следующим образом: уравнение изотермического распределения изотопов гелия при постоянной температуре T. Принципиальное отличие этих уравнений заключается в том, что температурная прямая отражает распределение изотопов
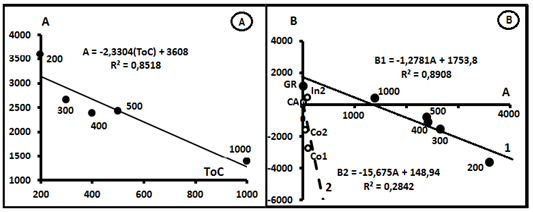
Рис. 9. А. Зависимость А от температуры. В. Компенсационные уравнения.

Рис.10. Вид температурной зависимости молярных концентраций гелия.
в одной пробе, тогда как изотерма характеризует распределение изотопов гелия в пробах из нескольких метеоритов. На рис.9.В – приведено компенсационное уравнение по температурам. Последнее говорит о том, что, несмотря на различное происхождение метеоритов и газов, источники газов имеют одинаковый начальный состав с параметрами 3Vo = 1,27815•10-8 cm3/г и 4Vo = 1753,8• 10-8 cm3/г (4Vo/3Vo = 1783,98 ≈1784 = K).
Проведём теперь термодинамический анализ. Для этого используем следующие обозначения. Если объём выделенного газа – V•10-8cm3/гп, ρ = 0,1785 г/дм3 - плотность 4He и ρ = 0,134 г/дм3 3He [16], то m =V•ρ - масса 4He = 0,0001785•10-8 г/гп (гп – грамм породы) и m = 0,000134•10-8 г/гп 3He; пусть М – молекулярный вес газа, то N = (m/М) - количество молей изотопов этого газа. Для двух газов с концентрациями N1 и N2 молярные доли их будем обозначать через M1 = N1/(N1 + N2) и M2 = N2/(N1 + N2). Тогда для изотопов гелия имеем соответственно М3 и М4. Определим вид температурной зависимости этих параметров для изученных изотопов гелия.
На рис.10 представлены типичные примеры выявленных зависимостей. По этим данным распределения концентраций изотопов гелия описывается полиномиальными уравнениями, имеющими вид (Mi – 3He или 4He)
lnMi = A(1000/ToK)2 + B(1000/ToK) + C. (3)
Результаты расчётов отражены в табл.5, а на рис.11 – диаграммы надкомпенсационных уравнений.
Таблица 5. Перечень полиномиальных уравнений.
|
Метеорит
|
Проба
|
A
|
B
|
C
|
R²
|
|
|
Изотоп 3He
|
||||||
|
Fayetteville
|
D1
|
2,0332
|
-8,4088
|
0,6802
|
0,9773
|
|
|
Fayetteville
|
D2
|
-0,6062
|
2,2127
|
-0,2236
|
0,9270
|
|
|
Renazzo
|
D2.
|
-5,0152
|
15,214
|
-16,421
|
0,8749
|
|
|
Nogoya
|
D1
|
0,0777
|
-0,0971
|
-7,8272
|
0,7629
|
|
|
Nogoya
|
D2
|
-2,1714
|
7,0169
|
-13,096
|
0,8495
|
|
|
Kapoeta,
|
D1.
|
1,7525
|
-8,229
|
1,4351
|
0,976
|
|
|
Kapoeta,
|
D1.
|
2,7512
|
-6,0955
|
-4,0781
|
0,892
|
|
|
Kapoeta,
|
D2.
|
-1,2866
|
5,3888
|
-13,318
|
0,9903
|
|
|
Kapoeta,
|
D3.
|
-9,0272
|
37,19
|
-40,014
|
0,9285
|
|
|
Kapoeta,
|
D4.
|
-3,2191
|
15,132
|
-22,474
|
0,9007
|
|
|
Изотоп 4He
|
||||||
|
Fayetteville
|
D2
|
-0,0001
|
0,0005
|
-0,001
|
0,8985
|
|
|
Renazzo
|
D2.
|
0,0003
|
-0,001
|
0,0002
|
0,9126
|
|
|
Nogoya
|
D1
|
0,0148
|
-0,0452
|
0,0276
|
0,7608
|
|
|
Nogoya
|
D2
|
-5,00E-05
|
8,00E-05
|
-0,0004
|
0,9301
|
|
|
Kapoeta,
|
D1.
|
0,0006
|
-0,0018
|
0,0009
|
0,9894
|
|
|
Kapoeta,
|
D1
|
-0,0008
|
0,0036
|
-0,0045
|
0,9556
|
|
|
Kapoeta,
|
D2
|
-0,0026
|
0,0057
|
-0,0037
|
0,8354
|
|
|
Kapoeta,
|
D3.
|
0,0001
|
-0,0006
|
0,0003
|
0,8625
|
|
|
Kapoeta,
|
D4.
|
-0,1048
|
0,2483
|
-0,1841
|
0,8248
|
|
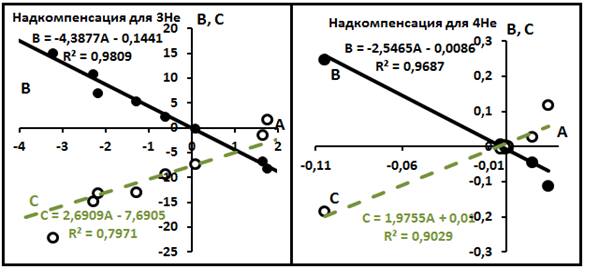
Рис.11. Надкомпенсационные уравнения для распределений изотопов гелия.
Отсюда намечаются следующие особенности распределений:
- иногда в пробах имеются по две фракции изотопов гелия; имеются пробы, для которых один из изотопов имеет соответствующее уравнение, то другой не имеет (например, Fayetteville-2, проба D1) (см. табл.5, 6).
- Как правило знаки коэффициентов при старших членах в уравнениях для 3He и 4He отличаются; направления, при которых ветви кривых идут вверх относительно осей координат, будем называть положительным, в другом направлении - отрицательным. Тогда для изотопа 3He 6 проб (~60%) из 10 имеют отрицательное направления кривых, для изотопа 4He – 5 проб из 9 (или ~ 55%). При этом, если для изотопа 3He кривая имеет одно направление, то для изотопа 4He – обратное.
Таблица 6. Уравнения распределения изотопов гелия в виде полных квадратов.
|
№№
П.п.
|
Метеорит
|
Про-ба
|
Уравнение
|
|
|
Изотоп 3He
|
||
|
1
|
Fayetteville-2
|
D1
|
ln(M3) = 1,6430((1000/ToK) -2,0322)2 - 8,123
|
|
2
|
Fayetteville-2
|
D2
|
ln(M3) = -0,6062((1000/ToK) - 1,8251)2 - 7,2044
|
|
3
|
Renazzo
|
D2.
|
ln(M3) = -5,0152((1000/ToK) - 1,5168)2 - 4,883
|
|
4
|
Nogoya
|
D1
|
ln(M3) = 0,0777((1000/ToK) - 0,6248)2 - 7,3023
|
|
5
|
Nogoya
|
D2
|
ln(M3) = -2,1714((1000/ToK) - 1,6158)2 - 18,765
|
|
6
|
Kapoeta
|
D1.
|
ln(M3) = 1,7522((1000/ToK) - 2,3476)2 - 7,9393
|
|
7
|
Kapoeta
|
D1.
|
ln(M3) = 1,6584((1000/ToK) - 1,1078)2 - 7,1705
|
|
8
|
Kapoeta
|
D2.
|
ln(M3) = -1,2791((1000/ToK) - 2,0843)2 - 7,4131
|
|
9
|
Kapoeta
|
D3.
|
ln(M3) = -2,278((1000/ToK) - 2,3791)2 - 1,8487
|
|
10
|
Kapoeta
|
D4.
|
ln(M3) = -3,2131((1000/ToK) - 2,3504)2 - 4,4099
|
|
|
Изотоп 4He
|
||
|
1
|
Fayetteville-2
|
D2
|
ln(M4) = 0,0003((1000/ToK) - 1,6667)2 - 0,0007
|
|
2
|
Renazzo
|
D2.
|
ln(M4) = 0,0148((1000/ToK) - 0,0248)2 + 0,0270
|
|
3
|
Nogoya
|
D1
|
ln(M4) = -5,00E-5((1000/ToK) - 0,8000)2 -0,0004
|
|
4
|
Nogoya
|
D2
|
ln(M4) = 0,0006((1000/ToK) - 1,5000)2 -0,0005
|
|
5
|
Kapoeta
|
D1.
|
ln(M4) = -0,001((1000/ToK) - 2,4000)2 - 0,0001
|
|
6
|
Kapoeta
|
D1
|
ln(M4) = -0,0034((1000/ToK) - 1,1176)2 - 0,0007
|
|
7
|
Kapoeta
|
D2
|
ln(M4) = -0,0009((1000/ToK) - 1,0000)2 - 0
|
|
8
|
Kapoeta
|
D3.
|
ln(M4) = -0,1048((1000/ToK) - 1,146)2 - 0,0370
|
|
9
|
Kapoeta
|
D4.
|
ln(M4) = 0,0242((1000/ToK) - 2,3285)2 - 0,0171
|
В табл.6 приведены результаты выделения полных квадратов по данным табл.5. Анализ преобразований показывает, что распределения мольных концентраций изотопов также описываются квадратными уравнениями вида
ln(Mi) = A((1000/T)2 – (1000/To) +B. (3)
Здесь параметры (1/То) и B характеризуют координаты вершины параболы, а A = (ΔH/R)2.
Отношения изотопов гелия – 4V/3V. В теоретической и практической геохимии СИЛЭ (стабильных изотопов лёгких элементов) используются, как правило, отношения концентраций изотопов (iС/jC), где С – содержание некоторого изотопа, причём в числителе, во-первых, располагается более тяжёлый изотопов, чем в знаменателе; а во-вторых, более тяжёлый изотоп распространён в природе намного меньше, чем изотоп в знаменателе. Как правило это отношение используется для определения температуры образования
Таблица 7. Сводные данные по зависимостям отношений изотопов He от T.
|
Минерал, метеорит
|
Регион, проба
|
A
|
B
|
C
|
R²
|
|
Берилл
|
Сибирь,
350 м.л.
|
-0,1698
|
0,645
|
14,918
|
0,9491
|
|
Волынь
1800 м.л
|
3,2687
|
-10,07
|
22,298
|
0,9156
|
|
|
3,4284
|
-9,9524
|
20,481
|
0,7406
|
||
|
Сподумен
|
|
4,8958
|
-13,738
|
21,424
|
0,8598
|
|
Kapoeta
|
D1
|
-2,7538
|
6,1012
|
4,0781
|
0,8927
|
|
D1
|
-1,7532
|
8,2325
|
-1,4358
|
0,9765
|
|
|
D2.
|
-0,8767
|
4,3433
|
2,8015
|
0,9702
|
|
|
D2.
|
-1,8196
|
3,5951
|
6,0001
|
0,833
|
|
|
D3.
|
-1,7829
|
7,994
|
-9,7695
|
0,9835
|
|
|
D4.
|
-7,4006
|
30,655
|
-23,254
|
0,7447
|
|
|
Fayetteville.
|
D2.
|
-0,9996
|
4,1611
|
3,7814
|
0,8073
|
|
D2.
|
-0,8577
|
4,4524
|
2,0533
|
0,7953
|
|
|
D1.
|
-0,5531
|
1,7014
|
6,2562
|
0,9575
|
|
|
Nogoya
|
D1
|
-0,3968
|
1,5458
|
6,5024
|
0,7449
|
|
D2
|
0,6883
|
-2,843
|
10,76
|
0,8495
|
вещества в природных условиях. В геохимии изотопов He мы будем использовать отношение 4He/3He = V4/V3, хотя более тяжёлый изотоп распространён намного больше. Это сделано для сравнения особенностейповедения изотопов He с особенностями поведения СИЛЭ. На рис.12 представлены примеры распределений отношений изотопов гелия с изменением температуры, а в табл.7 приведены
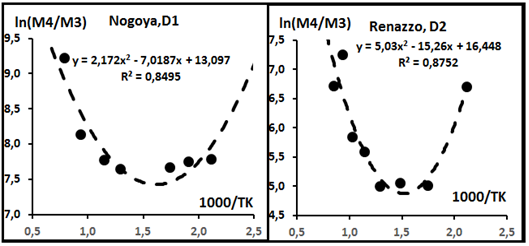
Рис.12. Температурная зависимость отношений изотопов гелия.
Таблица 8. Уравнения распределения отношений мольных долей изотопов гелия в виде полных квадратов.
|
Метеорит
|
Фация
|
Уравнения полных квадратов
|
ТооК
|
ΔH cal/M
|
|
Fayetteville
|
D1
|
ln(M4/M3) = -0,9996((1000/T) - 2,0814)2 + 8,1118
|
480
|
-818
|
|
Kapoeta
|
D1
|
ln(M4/M3)= -2,7538((1000/T) - 1,1078)2 + 7,4575
|
902
|
3591
|
|
Kapoeta
|
D1
|
ln(M4/M3) = -1,7532((1000/T) - 2,3479)2 + 8,2285
|
425
|
3677
|
|
Kapoeta
|
D2
|
ln(M4/M3) = -0,8767((1000/T) - 2,4771)2 + 8,1808
|
403
|
4394
|
|
Kapoeta
|
D2
|
ln(M4/M3) = -1,8196((1000/T) - 0,9879)2 + 7,7759
|
1012
|
-3295
|
|
Kapoeta
|
D3
|
ln(M4/M3) = -1,7829((1000/T) - 2,2419)2 - 0,8088
|
446
|
-2629
|
|
Kapoeta
|
D4
|
ln(M4/M3) = -7,4006((1000/T) - 2,0711)2 + 8,4910
|
482
|
-1985
|
|
Fayetteville
|
D2
|
ln(M4/M3) = 0,8577((1000/T) - 3,8650)2 - 10,934
|
258
|
-1741
|
|
Fayetteville
|
D2
|
ln(M4/M3) = -0,5531((1000/T) - 1,3788)2 - 5,2048
|
725
|
-2678
|
|
Nogoya
|
D1
|
ln(M4/M3 )= -0,3968((1000/T) - 1,9728)2 + 8,0468
|
506
|
-2652
|
|
Nogoya
|
D2
|
ln(M4/M3) = 0,6883((1000/T) - 2,0652)2 + 7,8243
|
484
|
-5402
|
водные результаты определения этих зависимостей, на рис.13 – надкомпенсационная диаграмма. В табл.8 – уравнения распределения отношений мольных долей в виде полных квадратов. Эти результаты свидетельствуют также о широком распространении полиномиальных (параболических) распределений изотопов гелия.
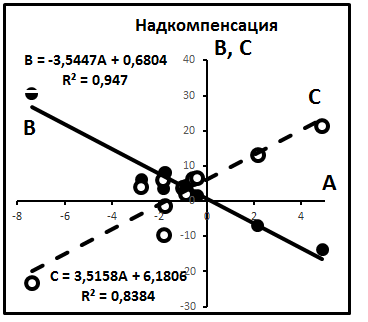
Рис.13. Надкомпенсационная диаграмма по материалам табл.7
Интерпретация полученных данных.
Физическая интерпретация.
Для объяснения подобной зависимости между изотопами He используем представления о параметрических уравнениях. Тогда можно написать:
Здесь xa и xc – параметры; a, b, c и d – постоянные величины. Для объединения уравнений нужно, чтобы xa = xc. Наиболее приемлемый вариант – xa = xc = ΔT. Тогда эти уравнения приобретают вид
Объединение этих выражений приводит к уравнению
Одним из вероятных процессов является зависимость объёмов газа от температуры, т.е. V = Vo(1 + βΔT), где β ≠ f(T)– температурный коэффициент объёмного расширения газа ([13] С. 27, 39). Запишем эти уравнения в виде:
Здесь 3Vo и 4Vo – начальные значения объёмов газов, обычно для Т=0оС. Тогда уравнение (1) приобретает вид (5)
(5)
Таким образом в уравнении (1)
Тогда уравнение (5) приобретает вид
(6)
Из этих уравнений следует:
Следствие 1. Если β4/β3 ≠ 1, то (4V/4Vo) = const·(3V/3Vo),
или (4V) = (3V) ·K·const. (7)
const = (1 + β4ΔT)/(1 + β3ΔT).
Приведём схему вывода. Для этого уравнения (4а) и (4b) перепишем в виде уравнений (4c) и (4d). Проведя умножение на
параметры, записанные за пределами квадратных скобках, разделив одно из уравнений на другое (вычтя из одного уравнения другое) и проведя необходимые преобразование, получаем нужный результат.
Следствие 2. Если β4/β3 = 1, то A = 4Vo/3Vo и B = 0. Отсюда β4 ≠ β3, поскольку во всех случаях В ≠ 0; кроме того, (4V/4Vo) = (3V/3Vo) или (4V/3V) = (4Vo/3Vo).
Следствие 3. При β4/β3 = 1 если 3V/3Vo = 1, то 4V/4Vo = 1.
Эти соотношения отражают физическую сущность параметров уравнения связи между изотопами гелия: параметры уравнений связи между изотопами гелия зависят от начальных значений содержаний этих изотопов и коэффициентов температурной зависимости объёмного расширения газа.
Считается, что для идеальных газов β = 1/273,16 = 0,003608. Для гелия, без учета его изотопов, β = 3,6579•10-3Т-1 [17] = β4, т.е. они оказались близкими. Но для других родственных газов Ar и Ne имеются другие данные: 3,676•10-3Т-1 и 3,761•10-3Т-1 [17] соответственно; поэтому можно высказать предположение о том, что эти газы могут быть неидеальными.
Проведём теперь грубую оценку величины β4/β3, используя уравнение (7), уравнения компенсации и изотерм и полагая, что угловой коэффициент AT изотермы описывается выражением (7):
AT = (4Vo/3Vo)·(1 + β4ΔT)/(1 + β3ΔT) = K·(1 + β4ΔT)/(1 + β3ΔT).
Изотерма 100оС: 4V = 3150,2(3V) - 304,15:
Термодинамическая интерпретация.
Термодинамическая интерпретация квадратных уравнений производится по методике, изложенной в работах [14, 15]. В таком случае A = (ΔHо/R)2, где ΔHо – энтальпия растворения газа в минерале (породе), R – универсальная газовая постоянная. Вынося число «1000» за скобки, это уравнение преобразуем к виду
ln(Mi) = (1000ΔHо/R)2 ((1/T) – (1/To)2 + ln(Mi)о. (8)
Полученные данные говорят об отсутствии связи между параметрами To и ΔHо. То же можно сказать и о связи между A и B.
Сопоставление одних и тех же параметров для обоих изотопов показывает хорошую сходимость между температурами To3, To4 и T, определённом по параметрам ln(M4/M3); это свойство хорошо иллюстрирует рис. 14.
Таблица 9. Сходимость между одноимёнными параметрами для обоих изотопов.
|
Метеорит
|
Про-ба
|
TooK
|
A
|
|||
|
ln(M3)
|
ln(M4)
|
ln(M4/M3)
|
ln(M3)
|
ln(M4)
|
||
|
Fayetteville
|
D2
|
799
|
600
|
548
|
-0,6062
|
0,0003
|
|
Nogoya
|
D1
|
1603
|
1250
|
514
|
0,0777
|
-5,00•10-05
|
|
Nogoya
|
D2
|
619
|
667
|
619
|
-2,1714
|
0,0006
|
|
Kapoeta
|
D1
|
426
|
426
|
426
|
1,7522
|
-0,001
|
|
Kapoeta
|
D1
|
903
|
895
|
902
|
2,7504
|
-0,0034
|
|
Kapoeta
|
D3
|
420
|
873
|
817
|
-2,278
|
-0,1048
|
|
Kapoeta
|
D4
|
425
|
425
|
425
|
-3,2131
|
0,0242
|
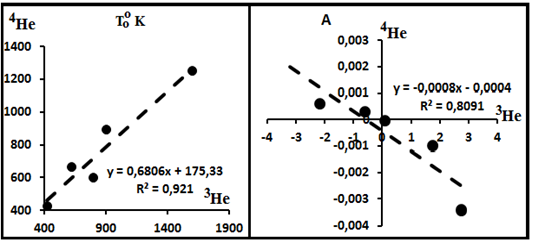
T(4He) = 0,6006T (3He) + 175,33 (R2 = 0,921).
Соотношения между параметрами A показаны на правой части рис.14. Они связаны уравнением
A(4He) = -0,0008 A(3He) – 0,0004 (R2 = 0,8091).
Поскольку A отражает энтальпию ΔH, на рис.14 наблюдается обратная зависимость между значениями ΔH для обоих изотопов.
Технология решения задачи о выделении полных квадратов позволяет дать приближённую интерпретацию уравнения надкомпенсации для изотопа 3He вида B = -4,3877A -0,1441 (табл.6, рис.11), которое можно представить в виде A + 0,2279B + 0,0328 = 0. В первом случае были введены два временных параметра- a (a2 = A) и В = 2ad (d = 1000/To). Тогда уравнение надкомпенсации приобретает вид a2 + 0,2279 (2d)a +0,0328 = 0 = a2 + (0,5558d)a + 0,0328, т.е. мы пришли к квадратному уравнению с переменной a. Подставляя сюда среднее значение d = 1,7884 (To ≈ 560oK), окончательно получаем a2 + 0,994a + 0,0329 = 0.
Корни этого уравнения найдём с помощью теоремы Виета для приведённого уравнения x2 + px + q = 0: x1,2 = (-p ± √D)/2, D = p2 - 4q. Подставляя сюда параметры искомого уравнения, получаем a1,2 = (-0,994 ± √(0,9942 – 4•0,0329))/2 = (-0,994 ± √(0,988 – 0,1316))/2 = (-0,994 ± 0,363)/2. Тогда a1 = - 0,6785; a2 = -0,315.
Выше показано, что (ΔHо/R)2 = 106А или ΔHо = 103aR. Тогда ΔHо1 ≈ -1348 кал/М, ΔHо2 ≈ -627 кал/М.
Второе уравнение имеет вид С = 2,6909a2 – 7,6905. Поставляя полученные значения a, получаем С1 = 2,6909(-0,6785)2 – 7,6905 = 1,2388 -7,6909 = -6,4517, откуда М31 =0,6452. С2 = 2,6909(-0,315)2 – 7,6905 = 0,2670 – 7,6905 = -7,4235, откуда М32 = 0,7424.
Повторим эти процедуры для изотопа 4He: первое уравнение надкомпенсации B = -2,5465A – 0,0086 или A + 0,3927B + 0,0034 = 0. Тогда получаем приведённое квадратное уравнение a2 + (0,7854d)a + 0,0034 или, подставляя среднее d = 1,3315 (To ≈ 750oK), a2 + 1,0458a + 0,0034. После применения теоремы Виета решение этого уравнения приобретает вид a1,2 = (-1,0458 ± √D)/2, D = 1,04582 – 4(0,0034) = 1,0937 – 0,0136 = 1,0801; √D = 1,0393. Тогда a1 = -1,0426; a2 = -0,0028. Отсюда ΔHо = 103aR: ΔHо1 = 103a1R ≈ -2072 кал/М; ΔHо2 = 103a2R ≈ -5,5636 кал/М.
Второе уравнение имеет вид С = 1,9755А + 0,01= 1,9755a2 + 0,01. Тогда С1 = 1,9755(-1,0426)2 + 0,01 = 2,1574; М41 = 0,2157. С2 = 1,9755(-0,0028)2 + 0,01 = 0,0100; М42 = 0,01.
Физический смысл значений этих параметров не ясен.
РАСПРЕДЕЛЕНИЕ ИЗОТОПОВ ГЕЛИЯ В ГЕОЛОГИЧЕСКИХ ОБРАЗОВАНИЯХ.
В заключении рассмотрим поведение изотопов гелия в природных образованиях. Изотопы гелия, как правило в паре с изотопами неона, изучены в метеоритах разных типов, а также изредка в объектах земной природы. Все анализы изученных объектов заимствованы из литературных источников: Виноградов А.П., Задорожный И.К. (1964 г.), Герлинг Э.К., Левский Л.К. (1956, 1960 г.), Лаврухина А.К., Колевов Г.М. (1965 г.), Baxter M., Funkhouser J. (1971 г.), Begemann F. (1965 г.), Bogard D.D., Nyquist L., Funk H. et al (1973 г.), Bogard D.D., Clark R.S., Keith E. et al (1971 г.), Eberhardt P., Geiss J., Grögler N. (1965 г.), Eberhardt P., Eugster O., Geiss J. et al (1966 г.), Eugster O. (1968 г.), Heymann D., Mazor E. (1968 г.), Hintenberger H., König H., Wänke H. (1962 г.), Hintenberger H., Wänke H. (1964 г.), Hintenberger H., König H., Wänke H. (19641, 19642, 1965 гг.), Hintenberger H., Schultz L., L., Wänke H. et al (1967 г.), Mazor E., Anders E. (1965 г), Mazor E., Heymann D., Anders E. (1970 г.), Nyquist L., Funk H., Schultz L., et al (1973 г.), Schaeffer O.A., Stoenner R.W. (1965 г.), Schultz L., Funk H., Nyquist L., et al. (1971 г.), Reynolds J.H. (1960 г.), Reynolds M.A., Simms L.A. (1973 г.), Zahringer J. (1962, 1968 г.) и др. Всего использовано около 800 анализов.
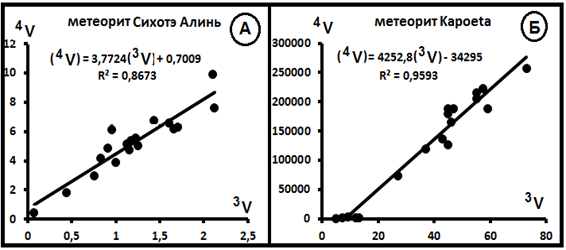
Рис.15. Гелий в метеоритах (тип 1). А- по материалам [18]. Б. То же [19].
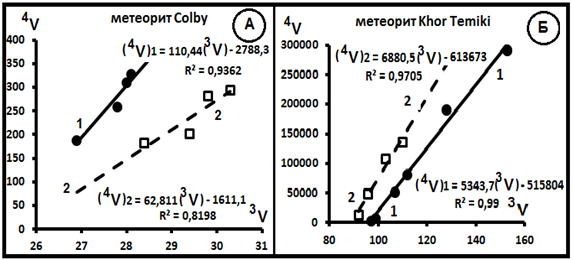
Рис.16. Гелий в метеоритах (тип 2). А-по материалам [20]. Б- то же [21].
Распределение изотопов гелия в отдельных метеоритах.
Всего было изучено 7 метеоритов: Сихотэ Алинь (18), Kapoeta (18), St. Germain (15), Moks (11), Colby (4+4), Khot Temiki (6+4), Indarch (5+3?), Grant (7). В скобках - количество полученных выборок и использованных для них анализов. Конечно этого мало для того, чтобы делать какие-то обоснованные выводы. Тем не менее какие-то предварительные заключения сделать можно. Выделяется три типа диаграмм.
Таблица 10. Сводные результаты анализа связей между изотопами He.
|
Метеорит
|
(4V) = A(3V) + B
|
R² =
|
N
|
Источник
|
|
Сихотэ Алинь (SA)
|
(4V) = 3,7724(3V) + 0,7009
|
0,8673
|
18
|
[18]
|
|
Kapoeta (Ka)
|
(4V) = 4252,8(3V) - 34295
|
0,9593
|
18
|
[19]
|
|
Colby (Co1)
|
(4V)1 = 110,44(3V) - 2788,3
|
0,9362
|
4
|
[20]
|
|
Colby (Co2)
|
(4V)2 = 62,811(3V) - 1611,1
|
0,8198
|
4
|
[20]
|
|
Indarch (In1)
|
(4V)1 = 20,025(3V) + 96,108
|
0,6322
|
5
|
[22]
|
|
Indarch (In2)
|
(4V)2 = 97,820(3V) + 425,23
|
0,9569
|
3
|
[22]
|
|
Khor Temiki (KT1)
|
(4V)1 = 5343,7(3V) - 515804
|
0,99
|
6
|
[21]
|
|
Khor Temiki (KT2)
|
(4V)2 = 6880,5(3V) - 613673
|
0,9705
|
4
|
[21]
|
|
Grant (Gr)
|
(4V) = 2,1047(3V) + 1172,2
|
0,9945
|
4
|
[23]
|
|
N-количество проб, использованных для построения диаграмм.
|
||||
В табл.10 приведены сводные результаты найденных связей между изотопами гелия.
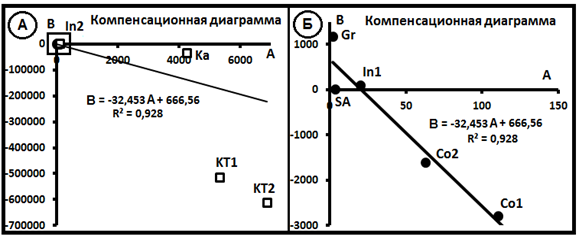
Рис. 17. Компенсационные диаграммы по метеоритам.
На рис.17 представлены компенсационные диаграммы по данным табл.10; на диаграмме около точек – краткие обозначения названия метеорита, расшифровку которых см. в табл.10. На рис.17А представлена обобщённая диаграмма. Она показывает, что в общем все пробы не образуют семейство, т.е. они не имеют общего источника гелия. В левом верхнем углу выделена часть диаграммы, которая в более крупном масштабе показана на рис. 17Б. Здесь уже вырисовывается частная компенсационная диаграмма, которая показывает, что согласно [12] вынесенные на неё пробы, возможно, имеют общий источник He состава 3Vo = 32,45E-8 см3/г породы и 4Vo =666,6E-8 см3/г.
Валовое распределение изотопов гелия.
На рис.18 приведено валовое, без разделения по группам, распределение изотопных составов гелия метеоритов. Выделяются три типа распределений:
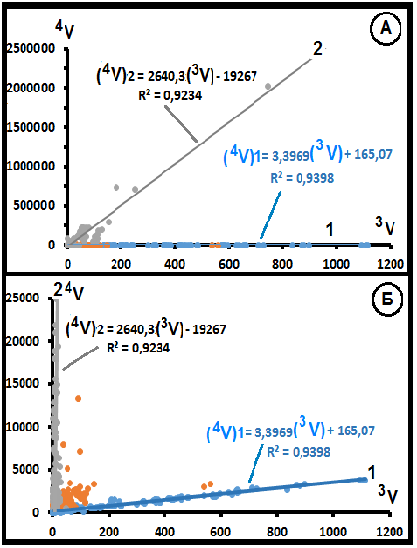
Рис.18. Валовое распределение изотопов гелия в метеоритах.
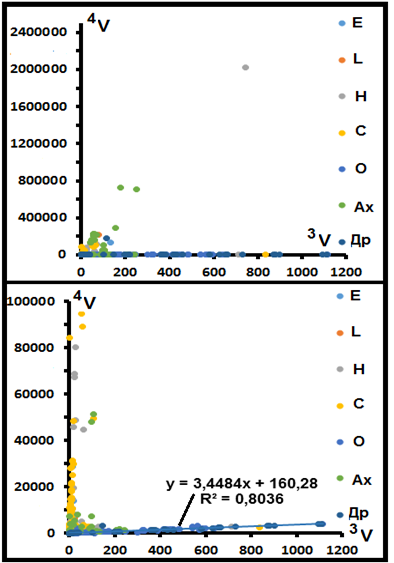
Рис.19. Валовое распределение изотопов He с учётом с разбиения метеоритов на классы и группы.
- Распределение первого типа (синий цвет) описывается уравнением 4V = 3,3969(3V) + 165,07. Оно охватывает 50,4% проб.
- Распределение второго типа (серый цвет) описывается уравнением 4V = 2640,3(3V) - 19267. Оно охватывает 29,1% проб. Распределение включает пробы с наивысшими концентрациями изотопов He.
- Распределение третьего типа (жёлтые точки) – компактное «облачное» распределение. Оно охватывает 20,5% проб. Этот тип распределений как правило характеризуется минимальными значениями концентраций обоих изотопов гелия.
На рис.19 это распределение приведено с разбиением проб по петрографическим группам метеоритов. На этом рис.19 Ах- ахондриты, Др.- Iron IIIF, Iron IIIB, Iron IC, Octahedrite, Iron IA, Iron IIB; О- железных метеоритов химического класса Ogg, Og, Om, Of, Opl.
Сопоставление рис.18 и рис.19 показывает, что метеориты первого типа распределения представлены преимущественно образцами групп О (основной), Др, L, намного меньше – E, С, H, Ах.
Метеориты с распределением второго типа представлены образцами преимущественно групп O и Др, С (основной), Н (основной), Ах.
С метеоритами третьего типа распределений связаны преимущественно образцы группы O, C, H. Для группы H типично распределение изотопов He второго и слабее третьего типов. Для метеоритов группы С распределения второго и слабее первого типов. Для метеоритов группы O – распределение первого типа.
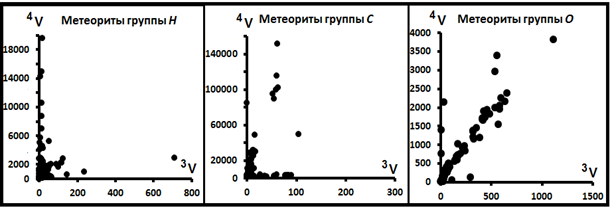
Рис.20. Характер распределения изотопов He в отдельных петрографических группах метеоритов.
Сопоставление верхних и нижних рядов рис.19 показывает, что метеориты первой генерации представлены преимущественно образцами групп О (основной), L, намного меньше – E, С, H, Ах. Сюда же попадают железные метеориты (Др). Метеориты второй генерации представлены образцами преимущественно групп железных метеоритов, С (основной), Н (основной), Ах. С метеоритами третьего типа связаны преимущественно образцы группы L, C, H. В таблице приведены данные, по которым построены диаграммы. В этой таблице строки I и II соответствуют упомянутым выше группам метеоритам. Строка III – это пробы, не вошедшие в эти группы.
|
Кол-во
|
Групы метеоритов
|
Всего
|
|||||
|
E
|
L
|
H
|
C
|
Ax
|
Fe-метеор
|
||
|
I
|
28
|
261
|
154
|
16
|
43
|
104
|
607
|
|
II
|
|
|
42
|
79
|
19
|
6
|
146
|
|
III
|
1
|
|
3
|
|
|
|
4
|
|
Всего
|
29
|
261
|
199
|
95
|
62
|
110
|
756
|
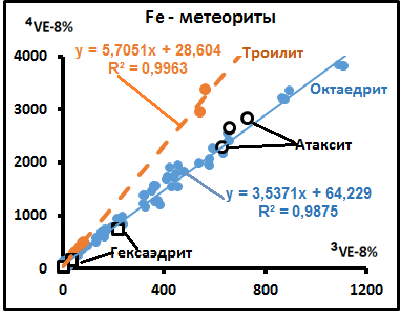
Рис.21. Поведение изотопов гелия в железных метеоритах.
На рис.21 приведено сводное распределение изотопов He в железных метеоритах, оно чётко описывается линейным уравнением 4V = 3,5371(3V) + 64,229 (R2 = 0,9875). Сопоставление с данными по изотопам свинца показывает отсутствие в гелиевых пробах выделяемых по свинцу групп метеоритов (рис. 23). Скорее всего это обусловлено тем, что в гелиевых группах пробы примерно на 90% были выполнены октаэдритами. Фиксируемые отдельные образцы атакситов и гексаэдритов полностью располагаются среди октаэдритов. Слегка выделяются троилиты, но и это, возможно, из-за малого количества образцов.
Таким образом по геохимическим свойствам метеориты подразделяются на две большие, существенно отличающиеся друг от друга группы. Нужно отметить, что эти геохимические группы выделяются и внутри отдельных петрографических групп. Примеры приведены на рис.20. Для группы H типично распределение изотопов He второго и слабее третьего типов. Для метеоритов группы С – распределения второго и слабее первого типов. Для метеоритов группы O – распределение первого типа
Приведённый материал позволяет формулировать две проблемы:
1). В литературе по отдельности изотопы He рассматривались совместно только с изотопами Ne, реже Ar. Были выявлены некоторые линейные зависимости, например,
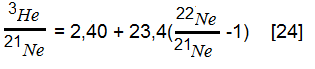
То же отмечается в [25]. В работе [20] дополнительно к [24] установлена линейная зависимость в паре
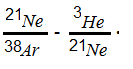
В работе [26] приводится выражение
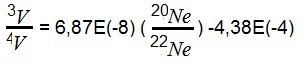
В космохимии главным механизмом образования изотопов He является радиоактивный распад урана или трития либо радиационное воздействие космических лучей на атомы более тяжёлых элементов. Пример первого распад урана U или трития T по схемам
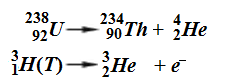
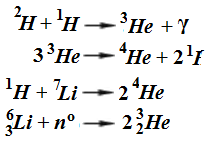
Здесь изотопы He выступают как продукты реакций. В следующих реакциях – как материал для образования других элементов:
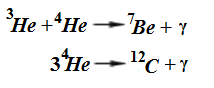
В работе [2] рассмотрены условия существования He в земных условиях и в космосе, факторы, влияющие на их распространение. Всё это с добавлением вида реакций, описанных выше, позволяют предположить, что все эти факторы не влияют или слабо влияют на динамику изменений взаимоотношений изотопов He друг с другом.
Альтернативой может быть предположение об общности поведения изотопов He с поведением других изотопов, стабильных и радиогенных, достаточно хорошо изученных. В последних основным фактором, влияющим на их поведение, являются физико-химические условия существования изотопов во вмещающих породах, прежде всего температуры.
2). Появление двух групп изотопов не является единичным случаем.
2a). При изучении распределений изотопов свинца также были установлены две группы анализов, особенно в координатах 207С - 204С, которые подтверждаются и в координатах ln206Pb- lniPb [29]. Это явление иллюстрирует рис.22.
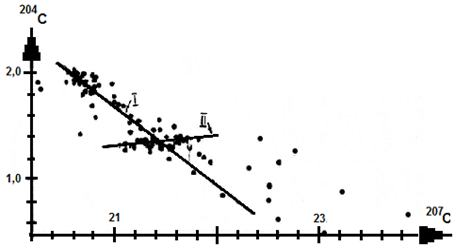
Рис.22. Группы свинца в метеоритах.
Первая группа (MP-I) характеризуется уравнениями: 204С= -0,094 206C + 3,751; 204С= -0,735 207С + 17,133; 204С = 0,095 208С - 3,600. Ее возраст - 4500 млн. лет (γ=0,5847) совпадает с другими независимыми определениями [31, 32].
Метеориты-II (см. рис. 21, Б, линия II) обладают параметрами: 204С = -0,080 206С + 3,320; 204С= 0,094207С - 0,630; 204С = 0,650 208С - 1,275.
Более наглядным является распределение изотопов Pb в метеоритах, представленное на рис. 23. На диаграмме наглядно видно разделение изотопов Pb две группы, описываемые уравнениями, приведёнными на рис.23. Согласно этим данным кажущийся возраст метеоритов первой группы 6000 млн. лет, второй – около 5400 млн. лет.
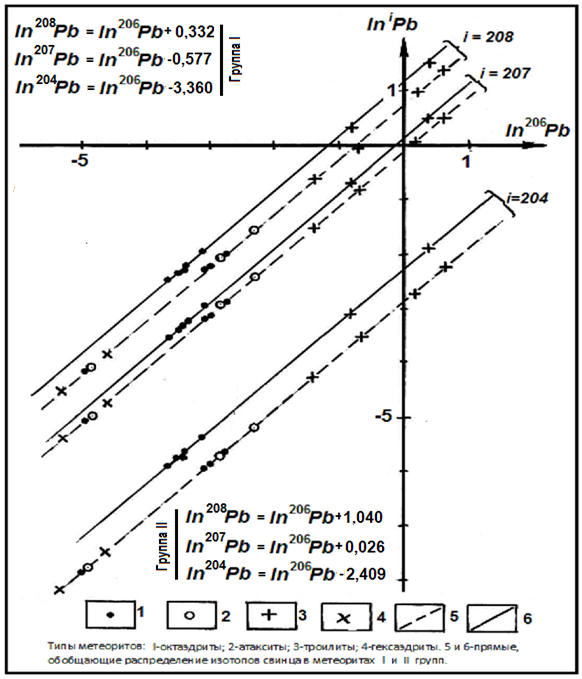
Рис. 23. Распределение изотопов Pb в железных метеоритах.
В заключении заметим, были изучены различные породы и метеориты в координатах ln 206Рb- ln iРb, где i - 207, 208, 204 (рис.23). Диаграммы всех изученных пород обладают общим свойством: это прямые с угловым коэффициентом s= 1.
Таблица 11. Средние значения изотопных отношений свинцов в различных геологических образованиях
|
Отноше-
ния
|
Принятые значения [32]
|
Полученные значения
|
|||
|
в земной коре (стр.44)
|
в Галакти-ке (стр. 35)
|
в метеорите
|
в поро-
дах
|
||
|
I
|
II
|
||||
|
208Pb/204Pb
|
35,338
|
38,905
|
39,258
|
22,199
|
38,475
|
|
207Pb/204Pb
|
15,270
|
1,586
|
15,959
|
7,925
|
15, 643
|
|
206Pb/204Pb
|
15,946
|
18,197
|
18,174
|
6,686
|
18,174
|
|
207Pb/206Pb
|
0,958
|
0,085
|
0,877
|
0,844
|
0,861
|
Результаты отражены в табл.11. Из таблицы видно, что выделяются две группы метеоритов, различающиеся изотопными отношениями изотопов свинца.
Дополнительную информацию о взаимоотношениях изотопов в геологических объектах даёт анализ приведённых уравнений вида Y = γX+ Γ (X = 206Pb/204Pb; Y = 207Pb/204Pb), по этим уравнениям и на рис.24 построены компенсационные уравнения по параметрам приведённых уравнений. По литературным данным собрана база данных. На диааграмму вынесены и обобщённые параметры распределений в целом по земным породам (из [41]).
Рис.24. Компенсационная диаграмма по параметрам приведённых уравнений.
Согласно [41] наличие компенсационных прямых говорит о том, что индивидуальные прямые пересекаются в одной точке (точке кроссовера), параметры компенсационной прямой отражают координаты точки кроссовера. Близкие трактовки отражены в [42]. На диаграмме чётко выделяются два семейства уравнений, соответствующих геологическим объектам (горные породы- интрузивные, осадочные, минералы и пр.) и метеоритам. Изотопные отношения свинцов горных пород описываются уравнением Γ = -17,747γ + 15,537; метеоритов Γ = -9,558γ + 10,437. Согласно [41] уравнения компенсации отражают результаты смешения как минимум двух компонентов. Тогда состав по крайней мере одного компонента описывается значениями изотопных отношений: для геологических объектов – Xo = 17,747, Yo = 15,537 (Yo/Xo = 0,875; кажущийся возраст - ~ 5,1 млрд. л.); для метеоритов –Xo = 9,558, Yo = 10,437 (Yo/Xo = 1,092; ~ 5,45 млрд. л.).
2б). В работе [33] приведено описание поведения изотопов неона в метеоритах. Было установлено, что распределение этих изотопов описывается следующими уравнениями:
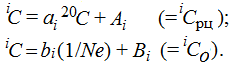
Здесь iСац – содержание радиационного, iСo – то же примесного неона. На рис. 24. представлены компенсационные диаграммы, построенные по этим уравнениям. Здесь a*i = 1/ai; A*i = -a*i iA.
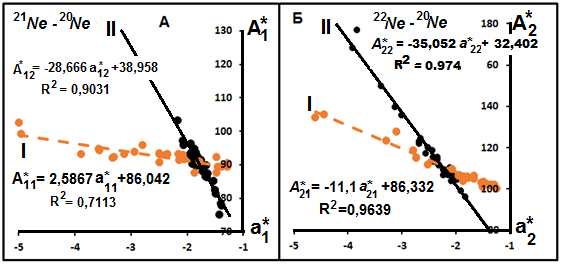
Рис.25. Компенсационные диаграммы для пар изотопов неона [23].
Эти диаграммы свидетельствуют о наличии двух генераций Ne. К сожалению по ряду технических не удалось привязать эти генерации к конкретным метеоритным классам и группам.
Таким образом среди изученных изотопов Pb, Ne, He наблюдается чёткое деление на две группы. Механизм этого разделения изотопов неясен.

Рис.26. Совмещённые компенсации изотерм и метеоритных распределений изотопов гелия.
На рис.26 приведены совмещённые компенсационные диаграммы изотерм и метеоритов из табл.10. Из неё видно, что наиболее близко к компенсационной диаграмме по изотермам приближается состав гелия метеорита Grant (Gr). Это позволяет в грубом приближении оценить температуру формирования изотопного состава He этого метеорита, используя зависимость от Т углового коэффициента А уравнения связи изотопов гелия. Уравнение температурной прямой - A = -2,3304(ToС) + 3608. Для метеорита Grant А= 2,104. Подставляя это значение в температурное уравнение, получаем оценочную температуру формирования изотопных соотношений ≈ 1500 – 1600оС.
ЗАКЛЮЧЕНИЕ
Проведённое изучение изотопного состава гелия выявило новые их геохимические свойства. Установлена неоднородность этих веществ как по составу, та и по физико-химическим свойствам. Выделяются несколько типов совместного распределений газов в теле изучаемого объекта, из которых главными являются: линейное, при котором точки группируются вдоль некоторой прямой линии типа y = Bx + C, и полиномиальное (параболическое), при котором распределение точек описывается уравнением y =Ax2 + Bx + C или A(x – xo)2 + C*. В ряде случаев выявлена физическая природа этих распределений. Для линейного распределения с A <0 такое распределение может быть вызвано либо механическим смешением компонентов (наиболее распространённый случай), либо особенностями распределения температур. Для линейных распределений выявляются компенсационные связи вида B = оC + p, говорящие, что концентрации газов являются не первичными, а продуктами смешения компонентов из источников более глубокого уровня.
Полиномиальное распределение lnMi =Ax2 + Bx + C (M – мольные доли изотопных компонентов i, x=1000/ToK, xo = 1000/TooK, 106A=(ΔH/R)2) связано с термодинамикой выделения газов из тела изучаемого объекта, позволяя оценить значение энтальпии растворения газа ΔHo в объекте и соответствующую ей температуру ТооK растворения. Многие полиномиальные системы связаны друг с другом через надкомпенсационные уравнения вида B = kA + l и C = mA + n, которые отражают термодинамические параметры существования газов в источниках более глубокого уровня. Проведённое исследование показало наличие возможности оценки решения задачи об источниках вещества газов, широко муссируемых в геологической литературе.
Литература.
- Хлопин В.Г. К геохимии гелия. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 176- 180.
- Якунин В.П. Геология гелия. Л.: Недра, 1968.
- Хлопин В.Г. Содержание гелия в Беломорской смоляной руде. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 219- 222.
- Хлопин В.Г. Методы определения геологического возраста, основанные на явлении радиоактивного распада. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 223- 240.
- Хлопин В.Г. К вопросу о содержании гелия в бериллиевых, борных и литиевых минералах. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 275- 276.
- Хлопин В.Г., Герлинг Э.К., Иоффе Э.М. Исследование выделения гелия из минералов и горных пород. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 181- 209.
- Хлопин В.Г. К вопросу об определении абсолютного геологического возраста по гелиевому методу на нерадиоактивных минералах с плотной кристаллической упаковкой. /Хлопин В.Г. Избранные труды. Т.II. Л.: Изд-во АН СССР. 1957. С. 277- 280.
- Толстихин И.Н, Друбецкой Е.Р. Изотопы гелия в породах и минералах земной коры. /Проблемы датирования докембрийских образований. Л.: Наука, 1977. С. 172-197.
- Black D. On the origins helium, neon and argon isotopic variation in meteorites. 1. Gas-rich meteorites, lunar soil and breccia. //Geochim. Cosmochim. Acta, 1972, 36, 3. P. 347-376.
- Black D.C. On the origin of trapped heliumь, neon and argon isotopic variations in meteorites. II. Carbonoceous meteorite. //Geochim. Cosmochim. Acta, 1972, 36, 3. P. 377-394.
- Reynolds J.H., Turner G. Rare gases in the chondrite Renazzo. //J. Geophis. Research, 1964, 69, 15, 3263-3281.
- Макаров В.П. «Явление компенсации» - новый вид связи между геологическими объектами. /Материалы I Международной научно- практической конференции «Становление современной науки – 2006». Днепропетровск, 2006. т.10, стр. 85- 115. URL: http://литология.рф/node/817.
- Сивухин Д.В. Общий курс физики. М.: Наука, 1979. 552 с.
- Макаров В.П. Нефть. Новые свойства: возгоны и полиномиальные ёуравнения. /Симпозиум: Наука и инновации в современном мире: Медицина и фармацевтика, биология, география и геология. Монография. Одесса: издание Куприенко С.В. 2017. С. 182-191. URL: DOI: 10.21893/978-617-7414-06-2.0. URL:http://литология.рф/node/1167
-
Макаров В.П. Экспериментальное изучение природного фракционирования изотопов аргона. /Труды Всероссийского ежегодного семинара по экспериментальной минералогии, петрологии и геохимии ВЕСЭМПГ -2019 Москва, 16–17 апреля 2019 г. С. 219-222. URL: http://www.geokhi.ru/rasempg/Shared%20Documents/2019/ТРУДЫ%20ВЕСЭМПГ-2019.pdf. URL: http://литология.рф/node/1201
- Гелий. URL: http://chemistlab.ru/publ/g/gelij/4-1-0-299
- https://www.fxyz.ru/справочные_данные/термодинамические_ свойства_веществ/коэффициент_объемного_расширения_газов/
- Герлинг Э.К., Левский Л.К. Продукты космической радиации в Сихотэ Алиньском метеорите. //Метеоритика, 1960, 18, 100-105.
- Zähringer J. Uber die uredelgase in den Achondriten. //Geochim. Cosmochim. Acta, 1962, 26, 6, 665-680.
- Nyquist L., Funk H., Schultz L. et al. He, Ne and Ar in chondritic in Ni-Fe as irradiation hardness sensors. //Geochim. Cosmochim. Acta, 1973, 37, 7, 1655-1685.
- Eberhardt P., Geiss J., Grögler N. Further evidence on the origin of trapped gases in the meteorite Khor Temiki. //J. Geophis. Research, 1965, 70, 17, 4375 -4378.
- Schaeffer O.A., Stoenner R.W. Rare gas isotope contents and K-Ar ages of minerals concentrates from the Indarch meteorite. //J. Geophis. Research, 1965, 70, 1, 209-213.
- Schultz L., Funk H., Nyquist L. et al. Helium, neon and argon in separated phases of iron meteorites. //Geochim. Cosmochim. Acta, 1971, 35, 1, 77-88.
- Eberhardt P., Eugster O., Geiss J. et al. Rare gas Measurements in 30 Stone meteorites. //Z. Naturforschune, 1966, 21a, 4, 414-426.
- Bogard D.D., Reynolds M.A., Simmas L.A. Noble gas cocentrations and cosmic ray exposure age of eight resently fallen meteorites. // Geochim. Cosmochim. Acta, 1973, 37, 11, 2417-2433.
- Mazor E., Heymann D., Anders E. Noble’s gases in carbonaceous chondriter. //Geochim. Cosmochim. Acta, 1970, 34, 7, 781-824.
-
Лаврухина А.Л., Колесов Г.М. Образование химических элементов в космических телах. М.: изд. мет. в области атомной науки и техники. 1962.172 с.
-
Герлинг Э.К. Нахождение в метеоритах инертных газов и их изотопный состав. //ДАН СССР, 1956, 107, 4, 559-561.
-
Макаров В.П. о природе обыкновенного свинца в минералах. //Отечественная геология. 5, 1994. С.67 – 77.
-
Шуколюков Ю.А., Горохов И.М., Левченков О.А. Графические методы изотопной геологии. М.: Наука, 1974. 207 с.
-
Найденов Б.М., Чердынцев В.В.,1967. Эволюция изотопного состав свинца Земной коры и железных метеоритов. //Геохимия,1967, 12, 1453-1457.
-
Войткевич Г.В., Мирошников А.Б., Поваренных А.С. и др. Краткий справочник по геохимии. М.: Недра, 1970. 278 с.
-
Макаров В.П. О стадийности образования неона в метеоритах. //Отечественная геология, 1995, 4, С. 58-66.
- Макаров В.П. Свинцовая изотопия и происхождение магматических пород. /Материалы конференции «Серии магматических горных пород – происхождение и металлогения». М.: изд. ИГЕМ, 1985. С. 21-22.
- Толстихин И.Н., Докучаева В.С., Каменский И.Л. Ювенильный гелий в древних породах. Гелий, аргон, уран и калий в Мончегорском плутоне (Кольский полуостров). //Геохимия, 1991, 8. С. 1146-1158.
- http://литология.рф/node/1201. Аргон. Анализ экспериментов по разделению изотопов.
- Макаров В.П. О стадийности образования неона в метеоритах. //Отечественная геология, 4, 1995. С.58 – 66.
- https://ru.wikipedia.org/wiki/Гелий
- https://ru.wikipedia.org/wiki/Аргон
- https://ru.wikipedia.org/wiki/Неон.
-
Найдёнов Б.М., Чердынцев В.В. Эволюция изотопного состава свинца земной коры и железных метеоритов. //Геохимия, 1967, 12, 1453 – 1457.
-
Нижний геохронологический рубеж Криворожской серии. Н.П. Семененко, Э.В. Соботович, Н.К. Ширинбеков и др. /Сб. Определение абсолютного возраста рудных месторождений и молодых магматических пород. /Материалы XVIII сессии комиссии по определению абсолютного возраста геологических формаций. М.: Наука, 1976. С.91 – 102.
Источник: Макаров В.П. Гелий. Вопросы геохимии благородных газов. /MATERIALS OF THE XVII INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE SCIENCE AND СIVILIZATION. V. 2. SCIENCE AND EDUCATION, SHEFFIELD, S YORKSHIRE, ENGLAND. ISSN 1561-6916, 2021. ООО Каллистон, 2021. С. 19 - 54.
Макаров В.П. Гелий. Вопросы геохимии благородных газов. /Материалы конференции "Проблемы научной мысли". Февраль №2, 2021. V.2. Днепр, ООО Каллистон, 2021. С.19 - 54. ISSN 1561 - 6916. Рег.№ 286319.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии