Нефть. Новые свойства. Некоторые особенности газовой фазы нефтяных месторождений.
НЕФТЬ. НОВЫЕ СВОЙСТВА. Некоторые особенности газовой фазы нефтяных месторождений.
Макаров В.П.
Введение.
Вопросы использования данных по природным газам с различных позиций рассмотрены в работах В.И. Вернадского (1912, 1931). В.В. Белоусова (1937), В.А. Соколова (1932, 1966, 1971, 1972), а также А.А.Карцева и В.П. Шугрина (1964), И.С. Старобинца (1957, 1963, 1965, 1966, 1968), Л.М. Зорькина (1973), Т.А. Ботнева (1966), А.А. Козлова (1950), Н.В. Кулакова (1972), В.П. Савченко (1935), В.П. Якуцени (1968) и др.[3]. В результате были даны обобщения результатов изучения газов, прежде всего, с точки зрения выявление геохимических критериев поиска залежей углеводородных флюидов (нефтей, газов, газоконденсатов) [3, 24].
Тем не менее, многие вопросы происхождения этих газов оказались недостаточно освещёнными, и, в частности, вопросы механизма связи газов между собой и их природа. Ранее [1, 2] для решения этих проблем на основе анализа свойства изверженных горных пород, нефти, углей, битумов и др., мы использовали новый метод обработки и интерпретации данных – метод компенсационных уравнений, опирающийся на корреляционный анализ. В результате получен материал, позволивший по-новому взглянуть на некоторые особенности образования и распространения углеводородов. Ниже эти приёмы использованы для изучения газовой атмосферы месторождений углеводородов. Для анализов использованы пробы газов, отобранные, в основном, из скважин, пробуренных в различных регионах СССР до 1970 годов. Все пробы изучены в местных лабораториях.
Наличие газовой шапки или оболочки над природными объектами – обычное явление, её состав весьма разнообразен и определяется составом и строением геологического объекта, с которыми они связаны. Общий состав газов изучен и описан достаточно полно во многих работах. Газовые шапки существуют и в связи с нефтяными месторождениями. Эти скопления газов объединяются в три группы:
-группа свободных газов, образующих крупные скопления вне пределов нефтяной залежи. Часто они самостоятельно слагают крупные газовые месторождения;
-группа газов, растворённых в самой нефтяной залежи;
-группа прочих свободных газов, поступивших в залежь из вмещающих пород за время жизни залежи и в большинстве случаев имеющих углеводородный состав с примесью некоторых акцессорных газов не углеводородного состава, связанных с условиями образования первых групп. Все анализы составов газов в изучаемых точках заимствованы из литературных источников.
Регионы исследований достаточно обширны и разнообразны: Урал (соли Березняковского месторождения), Урал, Предуралье, Дагестан, Предкавказье, Азербайджан, Украина (ДДВ), Тимано- Печорский НГБ, Волго- Уральский НГБ, Поволжье [Самарская (Куйбышевская) обл.], Западная Сибирь, Вилюйская синеклиза и т.д.
Набор газов включает CH4, C2H6, C3H8, n-C4H10, i-C4H10, n-C5H12, i-C5H12, n-C6H12, i-C6H12, СО2, N2, O2, Н2. Газовые пробы отбирались из солевых толщ, вод источников, газовых потоков свободных газов, трещинных газов, из гранитов, природных залежей, газовых месторождений и пр. Концентрации газов в подавляющем большинстве случаев измерялись в относительных единицах (объёмные и мольные %), значительно реже в абсолютных единицах-см3/кг породы. В методическом плане наблюдаются различные ошибки, осложняющие их обработку и интерпретацию её результатов. К ним относится, в первую очередь, произвол в выборе набора анализируемых газов, в интерпретации распространённостей газов, качественный и поверхностный характер этой интерпретации и пр.
Технология исследования полностью аналогична той, которая использована в предыдущих работах [1]. Так как метан – господствующий компонент в газовой шапке нефтяных месторожденияx, то он принимался за основной и его содержания откладывались по оси Х. Поскольку мы используем корреляционный анализ с построением корреляционных уравнений вида Y= AX + B, то составлялись пары (X-Y): CH4-N2; CH4-C2H6; CH4-C3H8; CH4-C4H10; (n-C4H10)-(i-C4H10), (n-C5H12)-(i-C5H12), редко (из-за отсутствия данных) СН4- СО2, N2- O2. Все вычисления проводились с использованием программы Excel. По этим данным рассчитывались параметры A и B уравнений Y= AX + B и по ним строились компенсационные уравнения вида B = ХоA + Yo, после чего интерпретировались выявленные компенсации. Группа индивидуальных выборок, объединённых компенсационной диаграммой, названа «семейством выборок». Теория компенсационного анализа отражена в [2]. Многочисленные примеры её использования приведены в работе [1] и др.
Основной текст.
Было создано 340 выборок, в каждую из которых входили от 4-5 до 20-30 проб. Выборки опираются на анализы 2200 проб газов. Большинство выборок отражено в таблице 1. Понятно, что эти данные не отражают истинных взаимоотношений между компонентами, прежде всего из-за несоблюдения методического единообразия при отборе и газовом анализе проб.
Таблица 1.Количество отобранных выборок.
|
№№ п/п |
Система (пары веществ) |
Связь |
Отно- шение |
Сум-ма |
|
|
есть |
нет |
||||
|
1 |
CH4-N2 |
66 |
23 |
0,35 |
89 |
|
2 |
CH4-C2H6 |
53 |
21 |
0,33 |
74 |
|
3 |
CH4-C3H8 |
39 |
16 |
0,41 |
55 |
|
4 |
CH4-C4H10 |
17 |
8 |
0,47 |
25 |
|
5 |
CH4-C5H12 |
4 |
3 |
0,75 |
7 |
|
6 |
CH4-C6H14 |
12 |
0 |
0 |
12 |
|
7 |
(n-i)C4H10 |
4 |
6 |
1,5 |
10 |
|
8 |
(n-i)C5H12 |
2 |
4 |
2,0 |
6 |
|
9 |
(n-i)C6H14 |
6 |
2 |
0,33 |
8 |
|
10 |
С2H6-C3H8 |
3 |
1 |
0,33 |
4 |
|
11 |
C2H6-C4H10 |
0 |
2 |
- |
2 |
|
12 |
C3H8-C5H12 |
1 |
0 |
0 |
1 |
|
13 |
C4H10-C5H12 |
2 |
0 |
0 |
2 |
|
Всего |
245 |
86 |
0,35 |
331 |
|
|
Примечание: на первом месте стоит соединение, откладываемое по оси Х. |
|||||
Семейство метан – азот.
На рис.2 приведена совместная компенсационная диаграмма проб, содержащих эту пару газов. Она включает пробы из различных регионов России и СССР, различного генетического типа: рудничные газы, газы нефтяных месторождений, водорастворённые газы, газы подземных и поверхностных вод вне нефтеносных областей и пр. Согласно табл.1 система CH4- N2 является самой распространённой, установлена практически во всех районах, содержащих в тех или иных количествах углеводороды.
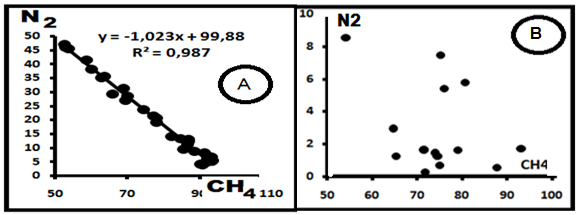
Рис. 1.Майкопские отложения Предкавказья. А.Наличие функциональнойсвязи. Б. Функциональная связь между компонентами CH4- N2 отсутствует.
Это обилие обусловлено, прежде всего, высокой распространённостью метана и азота, хотя согласно [5, 24] не отмечена связь концентраций этих газов с глубиной и литологией вмещающих пород. Эта комбинация является достаточно устойчивой. На рис. 1А и 1Б приведены примеры рядовых диаграмм, на рис.2 - сводная диаграмма для этой системы по материалам [4]. Для диаграммы рис.1А и 2 характерна тесная связь между газами, описываемая уравнением (в общей форме) CN2 = ACCH4 + B, и параметры корреляционных уравнений, высокий коэффициент корреляции R2; компенсационное уравнение имеет вид B= -89,45A + 4,404, R2 = 0,985. Здесь СN2 и CCH4– концентрации азота и метана в пробах соответственно. Всего выявлено 75 выборок и уравнений; из них в 6 уравнениях (8%) А>0, в остальных – А<0 и они имеют вид СN2 = -ACCH4 + B.
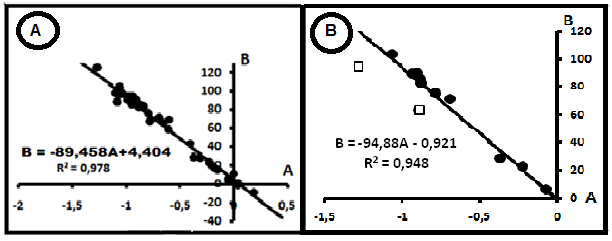
Рис.2.Компенсация распределений параметров индивидуальных прямых в системе СH4- N2. А. В целом для всей системы. В. Водорастворимые газы Нижнего Поволжья [9].
Интерпретация диаграммы затруднительна. Прежде всего, не ясна форма анализируемого азота, поскольку в природных условиях он может существовать не только в свободной форме, но и в связанном состоянии, например, аминах, аммиаках [4, 5]. Однако линейная с малой поперечной дисперсией связь позволяет ограничить влияние этих форм. Компенсация на рис.2 позволяет предположить общность механизмов существования метана и азота- это механическое смешение компонентов. Тогда параметры общего источника формирования смеси имеют значения: (CH4)o= 89,45%, (N2)o= 4,404%. Эту систему можно рассматривать в качестве эталона при анализе других систем. Однако наличие в одном и том же семействе выборок параметра A с положительными значениями не подпадает под действие правила смешения в варианте [2].
Семейство CH4 – C2H6
Является второй по распространённости (см. табл.1). Всего получено 63 уравнение вида C(C2H6) = AC(CH4)+B, C(CH4) и C(C2H6)– содержания в пробах метана и этана, из которых в 6 уравнениях A> 0 (≈11%), в остальных A < 0, т.е. имеют вид C(C2H6) = -AC(CH4)+ B. Типичные прямые линии представлены на рис.3 и 4.На рис. 4 представлена компенсационная диаграмма.
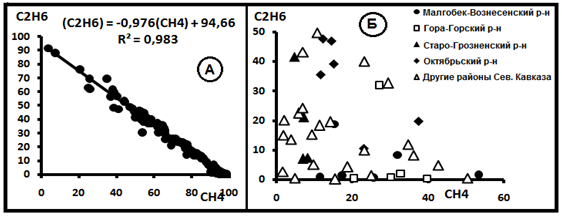
Рис.3. Зависимость содержаний метана и этана в свободно выделяющихся нефтяных и водорастворимых газах на Северном Кавказе. А-Наличие функциональной связи. Б. Функциональная связь отсутствует.
Уравнение C(C2H6) = -AC(CH4)+B также может быть представлено в форме C(C2H6)+AC(CH4)=B и рассматриваться как показатель наличия смешения компонентов. Тогда А = С(СН4)о = 91,37% и В= С(С2Н6)о = 3,92% отражают состав газовой смеси в источнике.
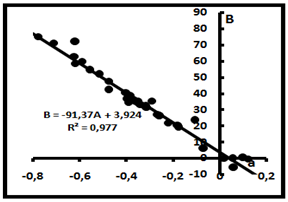
Рис.4. Компенсационная диаграмма для системы CH4-C2H6.
Особенностью этой системы является близость между углеводородами через принадлежность их к одной группе насыщенных углеводородов -алканам. Важно то, что метан образуется в высокотемпературных условиях при разложении или гидрирования этана, например, по реакции [7] с одновременным выходом этилена С2Н4 и водорода:
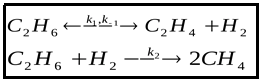
или пиролиза С2Н6 →С + СН4 + Н2.
Однако в экспериментальных условиях реакция проходит только при Т= 710- 830оС [7]. Сам этан разлагается при 485оС с образованием этилена и водорода по реакции C2H6 → C2H4 + H2 (575-650°C). Эти данные говорят о том, что выявленные закономерности не могут быть объяснены химическими реакциями между компонентами системы в высокотемпературных условиях.
В редких случаях содержания газов определялись в абсолютных единицах -см3/кг породы [18]. Для анализа их пересчитывали в молеклярные количества mi по формуле mi = Vidi/Mi, где Vi -измеренный объём газа в пробе i (см3/кг), di - плотность (г/см3) , Mi - молекулярный вес этого газа (г/Моль). Анализировались газ в газово-жидких включениях гранитов фундамента Западной Сибири и месторождений Белый Тигр и Драгон Зондского шельфа во Вьетнаме [18]. По этим данным были построены корреляционные диаграммы, представленные на рис. 5.
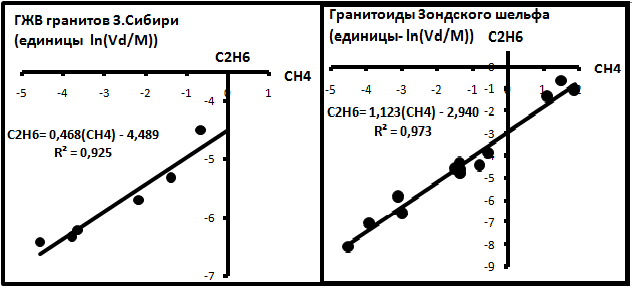
Рис.5. Газы ГЖВ гранитов.
Эти данные свидетельствуют о синхронности поведения метана и этана в природных условиях, т.е. с ростом содержания метана возрастает содержание и этана. Это позволяет предположить, что внешний источник газов, которые поступали в граниты, был с уже устоявшимися соотношениями газов.
Другие семейства углеводородов: СН4 - С3Н8, СН4 – С4Н10.
Третье по численности – семейство (СН4 – С3Н8). Только в двух уравнениях параметр A> 0(5,2%). Обладает теми же свойствами, что и предыдущие системы.
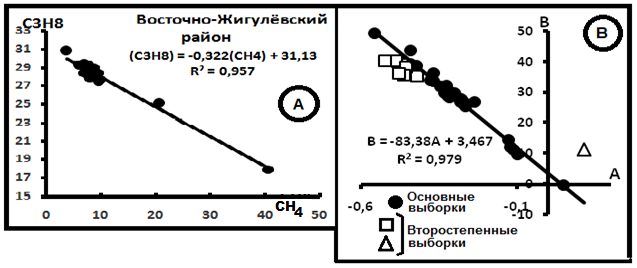
Рис.6. Примеры диаграмм в системе СH4-C3H8. А.Индивидуальная диаграмма распределения газов в Восточно-Жигулёвском районе[8]. В. Компенсационная диаграмма.
На рис.6 представлены графики распределений компонентов. Согласно им параметры смешения имеют значения: С(CH4)o = 83,38% и C(C3H8)o = 3,46%. Примеры распределений индивидуальных выборок в системе CH4–C4H10 показаны на рис. 7А. На рис.7В - компенсационная диаграмма в этой системе.
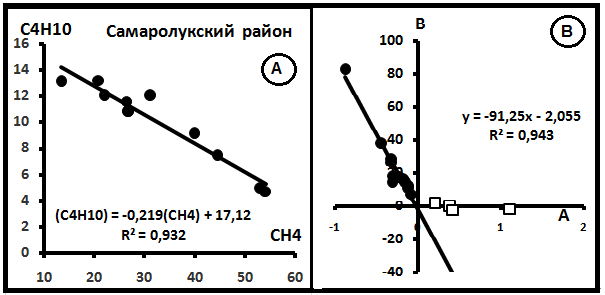
Рис.7. Примеры диаграмм в системе СH4-C4H10. А. Индивидуальная Диаграмма распределения газов в Самаролукском районе (Самарская обл.). [8]. В. Компенсационная диаграмма.
Семейства изомерных углеводородов (n-i) C4H10, (n-i)C5H12.
Запись вида (n-i)C4H10 означает наличие пары соединений n-C4H10 и i-C4H10. То же и с парой (n-i)-C5H12. Рассмотрены только два вида изомеров- бутаны и пентаны, по которым удалось собрать некоторое количество материала (см. таб.1; соединения 7, 8).
Семейство (n-i) C4H10.
На рис.8 приведены примеры связей между ними, а на рис.9 – компенсационная диаграмма изомеров (n-i)C4H10. Как видим поведение диаграмм резко отличается от поведения диаграмм для нормальных углеводородов, в частности, характерно наличие положительных значений параметра A. В таком случае возможно объяснение: они образованы в результате реакций вида … →(n-C4H10)+ (i-C4H10) +… Интерпретация компенсационной диаграммы пока не ясна.
Таблица 2.
|
№№ п.п |
Уравнение индивидуальной выборки. |
R2 |
Характеристика газа |
Исто-чник |
|
1 |
(C5H12)= -0,198(CH4) + 19,52 |
0,922 |
Попутные нефтяные газы, Азербайджан |
[10] |
|
2 |
(C5H12) = -0,26(CH4) + 23,21 |
0,962 |
Попутные газы, Предкавказье. |
[10] |
|
3 |
(C5H12) = -0,021(CH4) + 4,341 |
0,952 |
Попутные нефтяные газы. |
[11] |
|
4 |
(C5H12) = 0,092(CH4) + 1,457 |
0,862 |
Попутные нефтяные |
[11] |
|
5 |
(C6H14) = -1,164(CH4) + 94,17 |
0,957 |
Газ месторождений Саратовской обл. |
[14] |
|
6 |
(C3H8) = 0,465(C2H6) - 0,013 |
0,811 |
Газовые залежи. |
[11] |
|
7 |
(C3H8)= 0,937(C2H6) + 0,429 |
0,972 |
Башкирия, органи-ческое вещество карбонатов. |
[12] |
|
8 |
(C3H8) = 1,106(C2H6) + 2,062 |
0,954 |
Попутные нефтяные газы. |
[11] |
|
9 |
(C3H8) = 0,871(C2H6) - 0,746 |
0,975 |
Попутные нефтяные газы. |
[11] |
|
10 |
(C5H12) = 0,456(C3H8) - 0,233 |
0,891 |
Газовые месторож-дения. |
[8] |
|
11 |
(C5H12) = 0,412(C4H10) + 0,931 |
0,953 |
Попутные нефтяные газы. |
[11] |
|
12 |
(C5H12) = 0,603(C4H10) - 0,041 |
0,943 |
Газовые месторож-дения. |
[8] |
|
14 |
(СО2) = -0,712(CH4) + 67,31 |
0,878 |
Фонтанный газ. |
[10] |
|
15 |
(CO2-H2O) = -0,067(CH4) + 6,216 |
0,9 |
Каменноугольные отложения. |
[14] |
|
16 |
О2 = -0,281(CH4) + 26,02 |
0,969 |
Каменноугольные отложения. |
[14] |
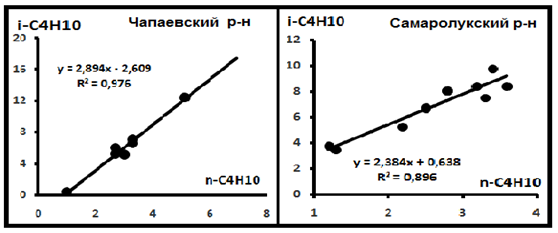
Рис. 8. Распределение изомеров в индивидуальных выборках Поволжья по материалам [8].
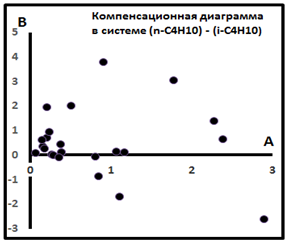
Рис. 9. Компенсационная диаграмма в семействе (n-i)C4H10 для индивидуальных выборок Поволжья [8].
Семейство (n-i)C5H12.
Примеры распределений изомеров показаны на рис. 10 и 11. Согласно рис.11 эти точки также не образуют семейство индивидуальных выборок, т.е. не имеют общего источника.
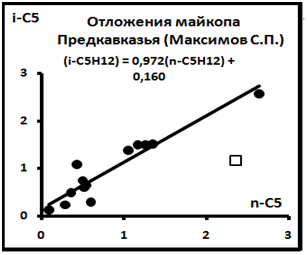
Рис. 10. Диаграмма распределений в системе(n-i)C5H12 по материалам[4].
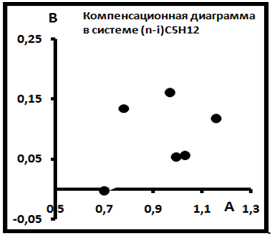
Рис.11. Компенсационная диаграмма в системе (n-i)C5H12.
Другие системы нами не рассматриваются из-за малого количества собранного материалы. Они приведены в таблице 2.
Сводная компенсационная диаграмма.
Сводная компенсационная диаграмма представлена на рис.12. Её свойства заключаются в том, что, во-первых, выделяются компенсационные диаграммы, описывающие четыре частных семейства, уравнения которых представлены в табл.3. Там же приведены и веса этих диаграмм, откуда видно, что намечается главная, генеральная, диаграмма, которая опирается на 76,2% всех выборок (табл.3).
Таблица 3.
|
№№ Прямой линии |
Уравнения линии компенсации |
R2 |
Кол-во выборок |
|
|
штук |
% |
|||
|
1 |
B1 = -91,354(A1) + 2,56 |
0,984 |
189 |
76,2 |
|
2 |
B3 = -39,831(A2) + 10,46 |
0,965 |
7 |
2,82 |
|
3 |
B2 = -71,799(A3) + 3,945 |
0,986 |
11 |
4,44 |
|
4 |
B4 = -4,7433(A4) + 6,035 |
6,0352 |
41 |
16,5 |

Рис.12. Сводная компенсационная диаграмма углеводородных газов.
Во-вторых, второе место занимает диаграмма, в подавляющем большинстве случаев сложенная индивидуальными диаграммами изомерныхуглеводородов - (n-i)C4H10 и (n-i)C5H12. она охватывает около 16% всех индивидуальных выборок. Выделяются также два второстепенных, акцессорных семейства, описываемые диаграммами №№2 и 3 с минимальным количеством индивидуальных выборок (табл.3).
В табл.4 приведена расшифровка семейства 2 и даны некоторые их характеристики. На рис. 13- детализация этого семейства. На диаграмме видно, что общая прямая линия разбивается на две частные прямые с уравнениями соответственно B1= -37,84(A1) +14,13 (R2=0,996) и B2= -42,22(A2) + 19,52 (R2=0,962). Цифры у точек соответствуют порядковым номерам
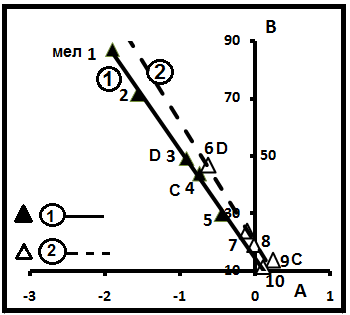
Рис.13. Детализация семейства 2.
Таблица 4. Расшифровка состава семейства 2.
|
№№ п.п. |
Семей-ства |
Индивидуальные выборки |
R2 |
Кол. проб |
Краткое описание |
Источ-ник |
|
1 |
1. |
(N2) = -1,902(CH4) + 87,04 |
0,448 |
12 |
Отложения Южно-Аламышикской площади. K. |
[15] |
|
2 |
1. |
(N2) = -1,561(CH4) + 71,34 |
0,863 |
8 |
Попутные нефтяные газы |
[11] |
|
3 |
1. |
(C2H6) =-0,907(CH4)+49,08 |
0,915 |
4 |
Кинель-Черкасский район, Михайловское месторождение, D. |
[8] |
|
4 |
1. |
(C3H8) = -0,7428(CH4)+ 43,73 |
0,726 |
4 |
Кинель-Черкасский район, Дмитриевское месторождение, C. |
[8] |
|
5 |
1. |
(C2H6) = -0,4394(CH4) + 29,6 |
0,903 |
8 |
Чапаевский район. Самарской обл. |
[8] |
|
6 |
2. |
(C3H8)= -0,6212(CH4)+ 46,75 |
0,944 |
6 |
Кинель-Черкасский район, Михайловское, D |
[8] |
|
7 |
2. |
(C2H6) = -0,105(CH4)+ 23,64 |
0,966 |
5 |
Майлисуйская антиклиналь |
[15] |
|
8 |
2. |
(C3H8)= -0,191(CH4)+ 19,04 |
0,957 |
29 |
Кинель-Черкасский район, Михайловскоеместорождение, D |
[3] |
|
9 |
2. |
(C2H6) = 0,2361(CH4)+ 13,55 |
0,549 |
9 |
Кинель-Черкасский район, Дмитриевское месторождение, C. |
[8] |
|
10 |
2. |
(C3H8)= -0,114(CH4)+ 11,35 |
0,780 |
14 |
Газовые залежи. |
[11] |
Таблица 5. Расшифровка состава семейства 3.
|
№№ п.п. |
Индивидуальные выборки |
R2 |
Кол. проб |
Краткое описание |
Исто-чник |
|
1 |
(N2) = -0,888(CH4) + 63,40 |
0,837 |
4 |
Воды нефтяных месторождений Куйбышевской, Саратовской и Оренбургской областей; D – C. |
[9] |
|
2 |
(N2) = -1,282(CH4)+ 95,23 |
0,703 |
17 |
Подземные воды Восточно-Русского артезианского бассейна; Ar - D. |
[9] |
|
3 |
(N2) = -1,180(CH4) + 87,11 |
0,921 |
7 |
Газы из солей Германии и Пермского края; P. |
[10] |
|
4 |
(N2) = -0,4936(CH4)+ 26,17 |
0,823 |
9 |
Дмитриевское месторож. Саратовская обл.; C. |
[8] |
|
5 |
(C4H10) = -0,3106(CH4)+ 14,15 |
0,689 |
26 |
Восточно-Жигулевский район. Самарская обл. |
[8] |
|
6 |
(C6H14) = -1,164(CH4)+ 94,17 |
0,957 |
18 |
Месторождения Саратовской области. |
[8] |
индивидуальных выборок в табл. 4. Там же приведена краткая геологическая характеристика и возраст вмещающих пород. Как видно, геологические характеристики не влияют на особенности диаграмм. Это соответствует известной точке зрения, высказанной, например, в работах [5, 10, 24] о слабой зависимости распределений содержаний газовых углеводородов от геологической обстановки.
В табл. 5 и на рис. 14 дана расшифровка семейства 3. Здесь наблюдаются те же особенности, что и на диаграмме семейства 2 (рис. 13). Во-вторых, в главную диаграмму входят частные диаграммы семейств СН4-N2, CH4-C2H6, CH4-C3H8, CH4-C4H10, CH4-C5H12, CH4-CO2, CH4-O2 (табл.6). Хотя они обладают различными свойствами, тем не менее, объединяются в единое генеральное семейство.
В-третьих, особое внимание заслуживает семейство 4, сложенное индивидуальными выборками изомерных углеводородов (70%). Это изомеры (n-C4H1) –(i-C4H10) (49%), (n-C5H12)- (i-C5H12) (15%) и (n-C6H14)-(i-C6H14)(6%). Ни одна выборка изомеров в другие семейства не попадает, хотя отдельные представители последних всё же в семействе 4 как примеси наблюдаются (30%): CH4-C2H6 (6%), CH4-C4H10 (8%), CH4-C5H12 (2%), C2H6–C3H8 (8%), C4H10–C5H12 (4%), C3H8–C5H12 (2%).
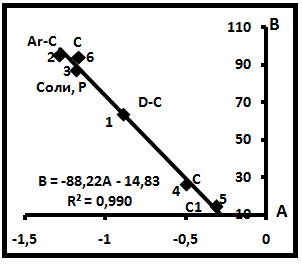
Рис.14. Расшифровка диаграммы семейства 3.
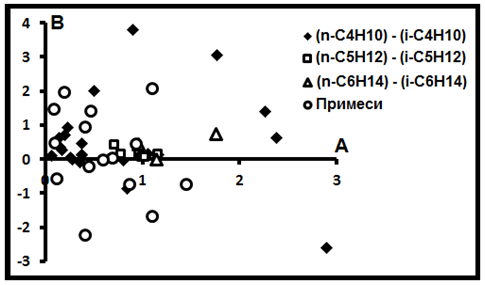
Рис.15. Газы - изомеры.
Детальное рассмотрение показывает, что это семейство, в отличие от предыдущих, не представляет единого целого, т.е. они не имеют единого источника. Все элементы семейства слагают облако не ясной формы (пример - рис.9, 11, 15). Точное соотношение между ними не известно. Особенности расположения её компонентов на сводной диаграмме (рис.12) обусловлено резким различием координатных масштабов.
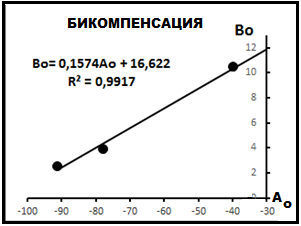
Рис.16. Бикомпенсация газов.
Данные рис.12 и табл. 3 позволяют построить так называемую бикомпенсационную диаграмму [2], представленную на рис.16. Физический смысл этой диаграммы не ясен. Однако известно, что по физическим свойствам она аналогична диаграмме индивидуальной выборки [2].
Обсуждение
Проведённые исследования показали, что все газы можно разделить на два множества: газы, которые аналитически связаны с другими газами, и газы, которые на координатной плоскости образуют облака неопределённой формы
Газы первого множества методом компенсации разделены на четыре подподмножества. Эти подмножества отражают наличие явления смешения составных частей газов, причём у значительной части газов (семейство 1) составы источников были близки друг другу (см.табл.6), поэтому на совместной диаграмме частные компенсационные диаграммы совпадают.
Таблица 6.Сводные данные по компенсационным уравнениям семейства 1.
|
№№ п.п |
Подсистемы |
Уравнение компенсации |
R² =
|
Состав источника |
|
|
Ao= (CH4)o |
Bo |
||||
|
1 |
CH4- N2 |
B= -91,044A + 0,8321 |
0,9845 |
91,04 |
(N2)o=0,832 |
|
2 |
CH4- C2H6 |
B = -96,093A + 1,2815 |
0,9892 |
96,09 |
(C2H6)o=1,989 |
|
3 |
CH4–C3H8 |
B = -76,443A + 4,8528 |
0,9555 |
76,44 |
(C3H8)o=4,852 |
|
4 |
CH4–C4H10 |
B = -91,605A - 0,8374 |
0,9761 |
91,61 |
(C4H10)o=0,837 |
Природа первого семейства CH4- N2 не ясна прежде всего из-за резкого различия свойств компонентов множества. Согласно [5,10] азот имеет достаточно много источников, начиная от биохимического разложения органических остатков и заканчивая высокотемпературными формами, связанными с магматическими очагами (эндогенные очаги) [10]. Чётких и строгих критериев их разграничения не существует. Считается, что связь с водородом свидетельствует об эндогенном источнике, связь с аргоном – о воздушном происхождении, если отсутствует- биохимический источник [5].
У метана намечается пять основных источников: разложение углеводородов нефти, разложение углей, рудничный газ и биохимическое низкотемпературное разложение органики в болотных системах (болотный газ). Пятый источник – выделение метана на дне океанических бассейнов, который связывают с поступлением метана из глубин земной коры и донными газогидратами. Здесь также нет чётких и строгих критериев их разделения. В настоящее время в обоих случая оценка источников осуществляется на основе субъективной точки зрения исследователя. В конкретном случае в газах, если и есть аргон и другие редкие газы, то вместе с азотом координатные очки образуют облако неопределённой формы. То же и с водородом: его либо почти нет, либо – облако неопределённой формы с весьма низкими его содержаниями.
Физический смысл уравнений вида СN2 = ACCH4 + B соответствует смешению компонентов в условиях, когда общая сумма концентраций компонентов постоянна. Вывод уравнения на примере распределения Fe и Mg в гранатах приведён в работе [23]. Это возможно либо, когда один элемент замещает другой, либо при разложении соединения, когда один компонент исчезает и появляется другой, например, АБ = А + Б: АБ исчезает в процессе разрушения, а вместо него появляются компоненты А или Б, позволяя создавать соответствующие пары. Соотношение компонентов реакции в этом случае определяется константой равновесия реакции.
Известны (искусственные) неустойчивые соединения типа азометана (С2H6N2), диазометана (CH2N2), азобензола (C11H11N2), нитрометана (CH3NO2) и пр. В естественных природных условиях они не известны. К тому же против азометана говорит тот факт, что при нагревании до 450оС он разлагается на чистый азот и этан [5], а не метан. Таким образом, метан, скорее всего, в газах не образует природных химических соединений с азотом.
Для каждой конкретной индивидуальной выборки уравнение смешения имеет вид N2 = A(CH4) + B, где в подавляющем большинстве случаев величина А< 0, хотя изредка бывает, что А> 0. С учётом первого свойства - это уравнение можно переписать в виде N2 + A(CH4) = B, т.е. это замкнутая бинарная система с ограниченными пределами изменения концентраций азота и метана в потоке. Ограничения определяются параметрами A и B. Таким образом, в данном случае имеет место механическое смешение метана и азота не ясной природы. Состав источника определяется значениями компонентов: (CH4)о = 89,45%, (N2)o = 4,404%.
Другие системы с метаном обладают теми же свойствами, но для них общее то, что, во-первых, они принадлежат единому семейству углеводородов, а во-вторых, при разложении у всех (С2H6, C3H8, C4H10, C6H14) конечными продуктами могут быть метан и водород. Однако в реальных условиях водорода настолько мало, что по мнению Н.В. Куликова [24] многие реакции разложения углеводородов проистекать не могут. Однако здесь допустима и другая интерпретация. Если опираться, например, на уравнение гидрирования этана С2H6 + H2 = 2CH4, то можно говорить, что весь водород ушёл на формирование метана из этана, а имеющийся водород, измеренный в образцах является уже остаточным. То же можно сказать и о других уравнениях образования метана, в левой части которых присутствует водород.
Семейство изомеров отличается от вышеперечисленных, во-первых, прежде всего тем, что не имеют общего источника, а во-вторых, положительными значениями параметра А. На рис.12 создаётся впечатление о наличии линейной связи между компонентами. Но это впечатление обманчиво, детальная расшифровка этой зависимости на рис. 9 и 11 показывает, что, обманчивость обусловлена резким различием масштабных разбиений координатных осей: сильным растяжением по оси X и сжатием- по оси Y. Первое свойство понятно: источником являются конкретные нормальные алканы. Второе свойство позволяет высказать предположение, что выявленные диаграммы индивидуальных выборок отражают наличие реакционных взаимоотношений между изомерными и нормальными алканами, например, по реакции n-C4H10→i-C4H10 (при наличии термодинамического равновесия ΔHреак.298оK = -6,9; ΔHреак.300оK = - 8,4кДж/М [16]).
В промышленности эта реакция осуществлялась «на хлористом алюминии, промотированном хлористоводородной кислотой»[16], при 50- 150оС в газовой и жидкой фазах. Ранее использовался катализатор СИ-1 (циркон/цеолитный) при температурах 250- 289оС [16].
Таблица 7. Продукты изомеризации бутана.
|
Температура,оС |
Содержание бутана, доли |
Отношение i-бутан/n-бутан |
|
|
n-бутан |
i-бутан(2-метилалкан) |
||
|
27 |
0,18 |
0,82 |
4,56 |
|
227 |
0,45 |
0,55 |
1,22 |
|
427 |
0,59 |
0,41 |
0,69 |
В табл. 7 приведены результаты изомеризации бутана. Эти данные показывают, что с ростом Т количество i-C4H10 падает, т.е. изомеризация является процессом низкотемпературным. Приведённая реакция характеризуется коэффициентом равновесия Kr в некоторой точке j:
Krj = aij/anj ≈ mij/mnj,
где ai и an – активности соответственно изомерной и нормальной разности бутана, которые, согласно [18], можно заменить на молекулярные количества mj; n и i– индексы, отражающие наличие изомеров бутана. Кроме того, известно [18], что
RTjlnKrj= -ΔGj, или lnKrj= -ΔGj/RTj =-Bj.
где ΔG- свободная энергия Гиббса (изобарно-изотермический потенциал), R–универсальная газовая постоянная, Т- абсолютная температура, оК. B = ΔG/RT. При работе на плоскости это равенство преобразуется в уравнение
lnKr= -ΔGr/RT =-B.
Подставляя значения Kr, получаем (стандартное) уравнение (изотерму)
ln(mi/mn)= -B или lnmi = lnmn –B.
в результате получили уравнения, близкие экспериментальным. Как видно, это уравнение прямой линии на плоскости с угловым коэффициентом s=1.
Так как содержания газов выражались в объёмных процентах, то для более точного сравнения пересчитаем исходные данные так, чтобы можно было использовать полученные уравнения. Для примера использованы данные по анализу газов в газово-жидких включениях гранитов фундамента Зондского шельфа на месторождении Белый Тигр (Вьетнам) [19]. Содержания газов выражались в см3 на 1 кг породы (см3/кг). Пересчёт проводился по формуле Vd/M. Согласно [20] для изомеров бутана М = 58,12; d = 0,551 и 0,573 г/см3 при 25оС соответственно для i-C4 и n-C4. Результаты обработки анализов отражены на рис.17. Результирующее уравнение имеет вид
ln(m(i-C4)) = 0,9701ln(m(n-C4))- 0,4526(R² = 0,939).
Полагая, что s = 0,9701 ≈ 1, получим, что экспериментальное уравнение тождественно теоретическому. Это позволяет предположить, в первом приближении, близость экспериментального уравнения изотерме и наличие термодинамического
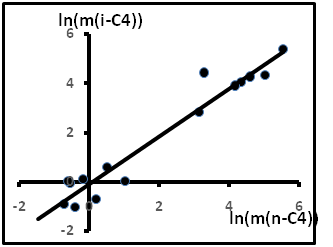
Рис.17. Содержания изомеров бутана в ГЖВ гранитов.
равновесия, а отсюда и равенства ΔG/RT = 0,453, или ΔG = 0,453RT.
Близкая ситуация с газами в Самаролукском (месторождения Зольненское, Яблоневый овраг, Жигулёвское – верхний девон - нижний карбон), Кинель-Черкасском (месторождения Михайловское и Коханское, средний-верхний карбон – нижний девон) районах и Западно-Рыбушанском месторождении Самарской(Куйбышевской) области [8]: соответственно lnm(i-C4)= 1,039lnm(n-C4) - 1,046 (R2= 0,933), lnm(i-C4) = 0,913lnm(n-C4) - 0,917 (R2= 0,847) и lnm(i-С4) = 1,079lnm(n-C4) - 1,015 (R2= 0,990). Все расчёты проведены по данным в молекулярных процентах, рассчитанных самими авторами работ. Эти данные позволяют предположить наличие между изомерами бутана термодинамического равновесия.
В былые годы в предположении наличия термодинамического равновесия соотношение между изомерами углеводородов было использовано для определения T образования нефти и углеводородных газов. Эксперимент провалился из-за того, что были получены T, изменяющиеся в очень широких пределах. В результате был сделан вывод об отсутствии этого равновесия, т.е. в природных условиях соотношения между изомерами углеводородов не являются равновесными [24, стр. 86-89]. Этот вывод стал официальным.
Однако, анализ этих работ [21] показал наличие нескольких методических ошибок: 1) анализ одиночных проб. Влияние этого фактора можно показать на следующем примере. На рис. 18 вынесена экспериментальная изотерма, построенная по данным измерения Tв пробах А, Б, В, Г, т.е. TА = TБ = TВ = TГ= Tи. Положение изотермы определяется углом α так, что tgα = f(Tи). При использовании одиночных проб, получаем значения tgαА = f(TА), tgαБ = f(TБ), tgαВ = f(TВ), tgαГ = f(TГ), как видно из рис.18 в этом случае, как правило, Tи≠ TА≠TБ≠TВ≠TГ, т.е. имеем различные Ti, которые могут существенно отличаться от истинной Tи. Постоянные любители этих ошибок - геохронология, геохимическая и изотопная баро- и термометрия.
2) Отсутствие доказательства наличия термодинамического равновесия.
3) При этом нет ни одной работы, в которой освещался бы механизм возникновения неравновесия. Нами были сделаны
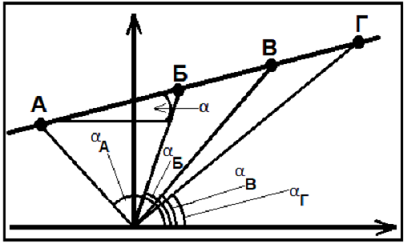
Рис.18. Экспериментальная изотерма.
попытки ответа на этот вопрос. Было показано, что в ряде случаев это может быть обусловлено наложением каких-то природных процессов, в частности - влиянием диффузии компонентов [21, 22, 23].
Попробуем оценить температуру образования изомеров бутана в гранитах. Для этого используем стандартные термодинамические данные (таб.8. [26]).
Таблица 8. Стандартные термодинамические данные изомеров бутана.
|
Углево-дород |
ΔHo298 кДж/М |
*ΔGo298 кДж/М |
So298 Дж/М•оК |
Cpo298 Дж/М•оК |
|
i-C4H10 |
-134,52 |
-222,32 |
294,64 |
96,82 |
|
n-C4H10 |
-126,15 |
-218,57 |
310,12 |
97,4 |
|
Реакция |
|
-3,75 |
|
|
|
*- рассчитаны по приближённой формуле: ΔGo298= ΔHo298- So298•Т[26] |
||||
Для гранитов была принята Тобр= 600оС = 873oK. Тогда ΔfGo873 =5,14кДж/М. Согласно этим данным равновесие между изомерами сдвинуто в левую сторону. Данные для графического решения проблемы приведены в таб.9 и на рис.18.
Таблица 9. Данные для расчёта Тобл.бутана.
|
№№ п.п. |
ТоК |
ΔGoТ Дж/М |
|
|
1 |
298 |
-3750 |
|
|
2 |
873 |
5140 |
|
|
3 |
100 |
|
377 |
|
4 |
500 |
|
1750 |
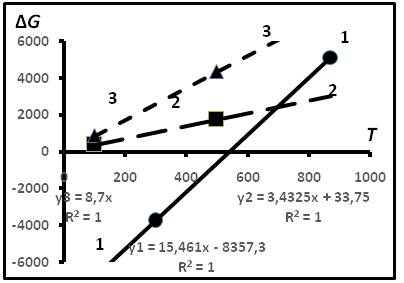
Рис.18.Схема решения задачи о температуре формирования равновесия между изомерами бутана в предположении линейности связи между параметрами. Прямая 1 соответствует теоретическим расчётам. Прямая 2- эмпирическим данным для ГЖВ гранитов. Прямая 3- эмпирическим данным для газов из газовых залежей.
В табл.9 первые два значения соответствуют теоретическим соотношениям ΔGoТ, вторые –эмпирические значения, полученные из соотношения ΔG = 0,453RT. Первые два значения соответствуют уравнению ΔG = 15,46Т- 8357, вторые ΔG = 3,432Т + 33,75. Ясно, что решением является точка пересечения прямых, описываемых этими уравнениями, для которой Т ≈ 424оС, соответствующая температуре термодинамического равновесия изомеров бутана. Данные для других объектов приведены в табл.10. Им соответствует прямая 3.
Таблица 10. Температуры образования бутанов.
|
№№ п.п. |
Регион. |
В |
Тобр.оС |
|
1 |
Белый Тигр (Вьетнам) |
0,453 |
424 |
|
2 |
Самаролукский район |
1,046 |
~960(?) |
|
3 |
Кинель-Черкасском район |
0,917 |
~960(?) |
|
4 |
Западно-Рыбушанском м-ж. |
1,015 |
~960(?) |
Вместе с этим были установлены объекты, в которых выполняются иные соотношения изомеров. Так в газах из нефтей Среднего Поволжья [25] установлены соотношения lnm(i-C4) = 1,7367lnm(n-C4) - 2,1313 (R² = 0,7714) для каменноугольной, lnm(i-C4)= 0,5699lnm(n-C4) - 0,5391(R² = 0,6895) и lnm(i-C4) = 0,7127lnm(n-C4)- 0,9007 (R² = 0,9645) для девонской нефтей. Полученные соотношения соответствуют общему уравнению
lnmi = Flnmn –B,
которое следует из реакции между изомерами бутана
(n-C4H10)→F(i-C4H10).
Оно отличается от стандартного теоретического. Расчитанные для них температуры оказались на уровне фантастических. Это говорит о влиянии каких-то наложенных процессов, природа которых не ясна. Возможная причина - миграционная неустойчивость бутана.
Что касается пентана и гексана, то они не могут быть оценены по описанной методике, поскольку в отличие от бутана у них больше изомеров, выделение которых в массовом порядке в пробах не производилось.
В таблице 8 приведены сводные данные, а на рис.18 – компенсационная диаграмма по эти данным для газов. Согласно им пробы газов располагаются вдоль компенсационной прямой с параметрами B=-1,292A + 0,211.
Таблица 8. Сводные данные для газов по форме lnm(i-C4) = Alnm(n-C4) + B.
|
Регион, месторождение |
A |
B |
Возраст отложений |
|
Запад.-Рыбушинское м-ние |
1,079 |
-1,015 |
Ниж.карбон- сред. верх.девон |
|
Кинель-Черкасский район |
0,913 |
-0,917 |
Ниж.карбон- сред. верх.девон |
|
Самаролукский район |
1,039 |
-1,046 |
Верх. девон- ниж. карбон. |
|
Среднее Поволжье |
1,736 |
-2,131 |
Каменноугольная нефть |
|
Среднее Поволжье |
0,57 |
-0,539 |
Девонская нефть |
|
Среднее Поволжье |
0,713 |
-0,901 |
Девонская нефть |
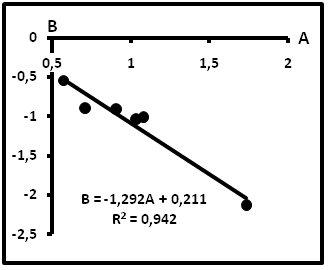
Рис.18. Компенсационная диаграмма по газам с абсолютными единицами измерения содержаний.
В газах из ГЖВ гранитов возможная их интерпретация заключается в следующем. Согласно полученным выше данным соотношения газов описываются уравнениями:
Западная Сибирь: lnmi(C2) = 0,468lnmi(C1) -4,489;
Месторождение Белый Тигр: lnmi(C2) = 1,123lnmi(C1) - 2,940.
Можно говорить, что в Западной Сибири на одну молекулу метана приходится две молекул этана, в Белом Тигре- на молекулу метана - одна молекула этана. Тогда возможные уравнения их образования имеют вид:
для Западной Сибири: C5H12 + 2H2 = 2C2H6 + CH4;
(пентан) (этан) (метан)
Для Белого Тигра: C3H8+ H2 = C2H6 + CH4.
(пропан) (этан) (метан)
В табл. 9 [25] приведены термодинамические параметры для стандартных условий, использованные при анализе полученных уравнений. Тогда для первого уравнения- ΔfGrо(298K) = -108,27 кДж/М; для второго - ΔfGrо(298K)= -60,25 кДж/М. Здесь (r) - реакция. Поскольку для обеих реакций свободные энергии имеют отрицательный знак, то реакции могут протекать в стандартных условиях.
Температура образования гранитов около 700оС ≈ 973оК. Состояние равновесия газов при этих условиях определяется по исходным данным, представленным в табл.9 [26]. Для этой температуры в первом случае ΔGo(973K)≈ ΔHo(298K)- 973∙ ΔSo(298K)=
Таблица 9. Стандартные термодинамические данные для изученных газов [26].
|
Соеди-нение |
ΔHo298 кДж/М |
ΔGo298 кДж/М |
So298 Дж./М.К
|
Коэффициенты уравнения теплоёмкости |
||
|
a |
b∙103∙T |
c∙10-5∙T2 |
||||
|
CH4 |
-74,85 |
-50,85 |
186,27 |
14,32 |
74,66 |
-17,3 |
|
C2H6 |
-84,67 |
-32,93 |
229,49 |
5,75 |
175,11 |
-57,85 |
|
C3H8 |
-103,85 |
-23,53 |
269,91 |
1,72 |
270,75 |
-94,48 |
|
C5H12 |
-146,44 |
-8,44 |
348,95 |
6,90 |
425,93 |
-154,39 |
|
H2 |
0 |
0 |
-75,90 |
26,94 |
0,0 |
0,79 |
- 74850 - 973х448,1 = -510851,3 Дж/Моль = -510,85 кДж/Моль, для второго - ΔGo(973K) ≈ ΔHo(298K) - 973∙ ΔSo (298K) = -271433 Дж/Моль = -271,4 кДж/моль. Таким образом, знаки при энергии Гиббса сохраняются, что говорит, во-первых, о непротиворечивости уравнений для этих условий, а, во-вторых, эта энергия значительно выросла по абсолютной величине, что говорит также о протекания этих реакций при более высоких температурах, т.е. об устойчивочти n-C3H10. Добавим, что по соотношению числа молей газов в обеих частях реакций обе реакция не зависят от давления P.
Заключение.
Таким образом, проведённый анализ показал, что в подавляющем большинстве случаев все индивидуальные выборки попадают на единую компенсационную прямую, характеризующую общий состав газа в источнике газов; выявленные соотношения между углеводородами основаны на их механическом смешении. Что касается изомеров, то для изомеров бутана установлено отсутствие общего источника, но выявлено наличие примерного термодинамического равновесия, которое в некоторых случаях нарушается влиянием наложенных процессов. Интерпретация данных по пентану и гексану невозможна из-за наличия бóльшего, чем у бутана, количества изомеров, которые в конкретных пробах не определялись. Показано, что газы в газово-жидких включениях гранитов предположительно образованы по реакциям: C5H12 + 2H2 = 2C2H6 + CH4 и C3H8 + H2 = C2H6 + CH4.
Дополнение.
Рассмотренные углеводородные газы обладают некоторыми особенными диффузионными свойствами. В работе [28] приведены коэффициенты диффузии и диффузионная проницаемость углеводородов в различных породах нескольких регионах России. Физические условия проведения экспериментов в работе [28] не указаны. В табл.13 приведены эти данные для изомеров бутана, а на рис.20А показан общий характер
Таблица 13. Коэффициенты диффузии изомеров бутана (см2/сек) различных породах.
|
Порода
|
lnD |
|
|
СН4 |
С3Н8 |
|
|
Московская синеклиза |
||
|
Доломит |
-4,880 |
-5,547 |
|
Доломит |
-5,915 |
-6,502 |
|
Известняк белый |
-5,655 |
-6,215 |
|
Северный Устюрт |
||
|
Глина с прослоями песчаников и алевритов |
-13,479 |
-15,053 |
|
Глина известковистая |
-11,959 |
-12,983 |
|
Глина известковистая |
-5,714 |
-6,215 |
|
Песчаник мелкозернистый |
-9,097 |
-10,078 |
|
Тунгусский бассейн |
|
|
|
Аргиллит трещиноватый, доломотизирован-ный, глубина 140 м |
-6,991 |
-7,621 |
|
Аргиллит загипсованный, глубина 222 м |
-8,759 |
-9,397 |
|
Аргиллит метаморфизованный, глубина 355 м |
-13,739 |
-14,014 |
|
Известняк плотный, глубина 430 м |
-15,987 |
-16,580 |
|
Южный Мангышлак |
|
|
|
Известняк плотный, глубина 35 м |
-10,597 |
-11,418 |
|
Глина карбонатная, глубина 82 м |
-10,771 |
-11,251 |
|
Мергель глинистый, глубина 222 м |
-7,729 |
-8,181 |
|
Мергель плотный, глубина 375 м |
-13,074 |
-13,553 |
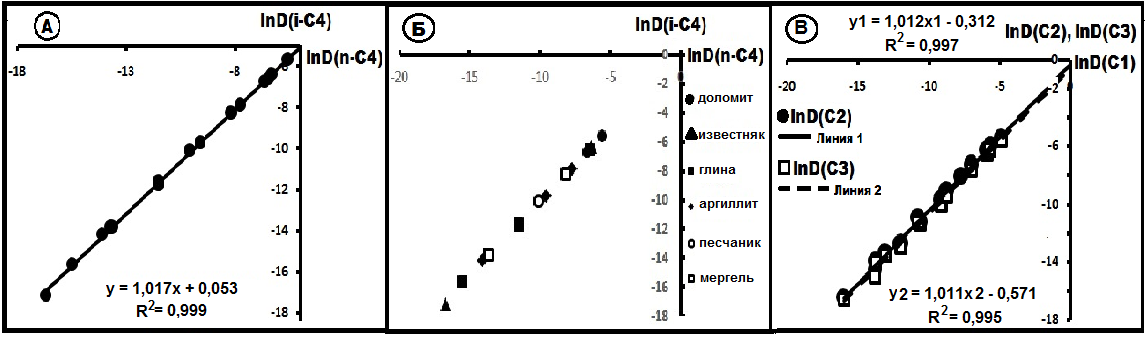
Рис. 20. Совместное распределение коэффициентов диффузии изомеров бутана и других углеводородов.
изменения коэффициентов диффузии по породам, представленных доломитами, известняками, аргиллитами, различными глинами из разных регионов России, а на рис.20Б- конкретно по породам. Несмотря на это разнообразие, все точки с минимальной поперечной дисперсией ложится на прямую линию с уравнением lnD(i-C4) = 1,017lnD(n-C4) + 0,053, R2 = 0,999, или в общем случае lnD(i-C4) ≈ lnD(n-C4) + F. Таким образом, хотя коэффициенты диффузии бутанов в этих породах резко различаются, в системном плане их совместное распределение описывается уравнением прямой линии. Это характерно не только для бутанов, но и для других углеводородов (см. рис.20В). Для последних уравнения прямых имеют вид:
lnD(C2) = 1,012lnD(C1) - 0,312;
lnD(C3) = 1,0112lnD(C1) -0,571.
Это явление достаточно точно можно описать, используя температурное уравнения Аррениуса для диффузии: D = Doexp (-E/RT), в котором Do- предэкспоненциальный множитель, E – энергия активации, R- универсальная газовая постоянная, T – температура, в данном случае ToK. Здесь возможны два подхода.
А). Пусть для двух газов D1 = Do1exp (-E1/RT1) и D2 = Do2exp(-E2/RT2). Прологарифмировав, вычтя второе уравнение из первого уравнения, проведя необходимые преобразования и положив Т1 = Т2, получаем уравнение
lnD1 = lnD2 + [ln(Do1/Do2) – (E1 – E2)/RT].
Это уравнение достаточно неудобно, поэтому перейдём ко второму случаю.
Б). Здесь также будем использовать логарифмические значения. Так как пробы газов отбираются из одной и той же пробы, то T1 = T2 = T и
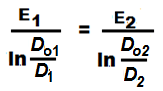
Его преобразование приводит к окончательному уравнению
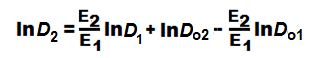
Из этого уравнения выявляется чёткая интерпретация параметров диффузии бутанов в гранитах: параметр С = (E2/E1), а F = lnDo2 – (E2-E1)lnDo1. Подставляя числовые значения, получаем (E2/E1) = 1,017, F = lnDo2 -1,017lnDo1 = 0,053. Для осадочных пород соответственно (E2/E1) = 1,012 и (E2/E1) = 1,0112, а также F = lnDo2-1,012lnD01 = -0,312 и F = lnDo2 - 1,0112lnDo1 = -0,571.
На рис.21 показана диффузионная проницаемость (в см2/с) этих же газов в логарифмическом масштабе по материалам [28]. Газы отбирались из углей различной степени метаморфизма (МК3, МК5, АК1, АК2) и пород: разной трещиноватости долериты, соли, галит. На рис.21А эти данные относятся к изомерам бутана. Все породы объединяются в единое множество, тогда как угли (МК3, АК3) резко от них отличаются. На рис.21Б – те же данные для пар СН4- С2Н6 и СН4- С3Н8. Как видим результат аналогичный. На рис.21Б угли уже не отличаются от пород. Кроме того, рис.21 показывает, что диффузионная проницаемость описывается уравнением Аррениуса.
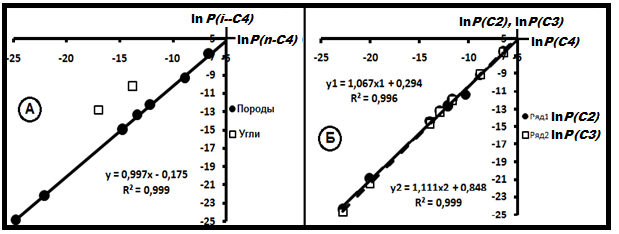
Рис.21. Диффузионная проницаемость изомеров бутана (А) и других углеводородных газов (Б). P- коэффициент проницаемости.
Поскольку понятие "диффузионная проницаемость" чётко не сформулировано, что видно при сопоставлении единиц измерения (в данном случае -см2/с, общепринятое - см2/с•атм), то интерпретировать эту зависимость достаточно сложно.
Литература.
1. Макаров В.П. Нефть. Основные свойства (сводные данные). //Симпозиум «Перспективные тренды развития науки». Монография: Медицина и фармацевтика, биология, география и геология. Глава 4. Князева М.В., Соколова Г.Г., Груздева А.А., Прокопюк А.В., Закамский В.А. Макаров В.П. Одесса: издание Куприенко С.В. 2016. С. 78 -100.
2. Макаров В.П.«Явление компенсации» - новый вид связи между геологическими объектами.//Материалы I международной научно-практической конференции «Становление современной науки-2006». Т.10. Днепропетровск: Наука и образование, 2006. С. 85-115.
Макаров В.П. Явление «компенсации» - новый вид связи между геологическими объектами. URL: http://www.lithology.ru/node/817.
3. Старобинец И.С.,Ломейко Н.Н. Извлечение и анализ рассеянных газов при геологических поисках залежей углеводородов. М.: «Недра», 1977.
4. Критерии прогноза качественного состава нефтей и газов. Труды ВНИГРИ, вып.223. Под редакцией С.П.Максимова. М.: Недра, 1981.
5. Якуцени В.П. Природные газы осадочной толщи. Ленинград: Недра, 1976. 344 с.
6. Трещина Н. И. Изучение нефтяных газов Терско-Дагестанской области.//Геологический сборник №1. Труды ВНИГРИ, Новая серия. Ленинград: Госгортехиздат, 1955. С.413-453.
7. Научные основы процесса пиролиза углеводородов. Термодинамика пиролиза углеводородов. URL: http://www.Ref→b.ru>look/2576269.html
8. Мжачих К. И., Тужилов Р. Ф., Мурашкина М. Д. и др. Справочник физико-химических свойств нефтей и газов, месторождения и разведочные площади Куйбышевской, Оренбургской, Ульяновской и Пензенской областей. Под редакцией С. Я.Вайнбаума. Куйбышев,1960. С. 179 - 204
9. Зингер А.С. Газогидрохимические критерии оценки нефтегазоносности локальных структур (на примере Нижнего Поволжья). Саратов: изд-во Саратовского университета, 1966. 476 с.
10. Соколов В. А. Геохимия земной коры и атмосфер. Геохимия природных газов. М.: Изд-во Недра, 1966. 302 с.
11. Соколов В. А. Новые методы разделения легких углеводородов. М.:Госгортехиздат, 1961. 331 с.
12. Неручев С.Г. Рассеянное органическое вещество на разных этапах литогенеза осадков и процессы нефтегазообразования. Труды ВНИГРИ. Л.: изд-во ВНИГРИ, 1978. 199 с.
13. Кузьмина О. А., Пантелеев Г. Ф., Кувшинова И. Ф., Исаенко В. Н. Геология и перспективы газонефтеносности Северной Туркмении и прилежащих районов Узбекистана. Труды треста Союзбургаз, вып.8. М.: Недра, 1970. 304 с.
14. Нефтегазоносность западной окраины Русской платформы. Труды ВНИГРИ, вып. 270. Л.: изд-во ВНИГРИ, 1969.
15. Симаков С. Н., Клейнберг В. Г., Воробьев А. А. и др. Геологическое строение и нефтеносность Ферганы. Труды ВНИГРИ, вып.110. Л.: Гостоптехиздат, 1957. 606 с.
16. Бекман И.Н. Мембраны в медицине. Курс лекций. Лекция 5. Молекулы газов: размер, форма, взаимодействие. URL: http://profbeckman.narod.ru
17. Кузьмина Р.И., Фролов М.П. Изомеризация – процесс получения экологически чистых бензинов. Саратов: изд. Саратов. ГУ, 2008. URL: elibrary.sgu.ru›Uch_Lit›161.pdf
18. Вуд Б, Фрейзер Д. Основы термодинамики для геологов. М.: Мир, 1981.
19. Шнип О.А. Углеводороды газово-жидких включений в минералах гранитоидов фундамента нефтегазоносных областей.// Геология нефти и газа. 2, 1997.
20.http://www.gazpromschool.ru/students/projects/alkans/alkani/alkani.htm
21. Макаров В.П. Некоторые условия образования низкотемпературных карбонатов по изотопным данным. / Материалы совещания «Проблемы литологии, геохимии и рудогенеза осадочного процесса». М.: 2000. Т.1. С.433-437.
22. Макаров В.П. О влиянии диффузии на формирования изотопного состава подземных вод./Материалы совещания «Фундаментальные проблемы нефтегазовой гидрогеологии». М.: изд-во ГЕОС (ИПНГ), 2005. С.513-517.URL: http://www.ipng.org.ru/conference/smej/sm10.pdf. http://www.hydropetroleum.ru/conference/smej/sm10.pdf.
Макаров В.П. О радиолитической природе алканов в соляных породах./Ежегодный семинар по экспериментальной минералогии, петрологии и геохимии (ГЕОХИ, г. Москва). URL: http://www.scgis.ru/russian/ cp1251/hdgggms/1-2009 /informbul-1_2009/ hydroterm -24.pdf.
23. Макаров В.П. «Уравнение компенсации» - новый метод решения задачи об источниках вещества на основе анализа петрохимии высокотемпературных образований (гранат, пироксен). /Ежегодный семинар по экспериментальной минералогии, петрологии и геохимии (ГЕОХИ, г. Москва). URL:http://www.scgis.ru/russian/ cp1251/h_dgggms/1-2008 /informbul-1_2008/mineral-20.pdf
24. Черненко Г.В. О методике определения температуры нефтеобразования. /Сб. Геология и разработка нефтяных месторождений. М.: Гостоптехиздат, 1961.
25. Формирование и размещение залежей нефти и газа. Ред. Н.В. Куликов. Труды НВНИИГГ, вып. 18. Саратов: изд-во Саратовского университета. 1972. 279 с.
26. Краткий справочник физико-химических величин. Ред. А.А. Равдель и А.М. Пономарёва. Л.: Химия, 1983. 232 с.
27. Духанин Г.П., Козловцев В.А.. Термодинамические расчёты химических реакций. Волгоград: изд-во ВОЛГ-ГТУ, 2010. 96 с.
28. Геохимические методы. http://mydocx.ru/2-17846.html.
Примечание: источник: Макаров В.П. НЕФТЬ.НОВЫЕ СВОЙСТВА. Некоторые особенности газовой фазы нефтяных месторождений. Материалы международной конференции: Перспективные достижения современных учёных. Монография: Экономика, менеджмент, география и геология, архитектура и строительство. Сушко О.П., Богданова О.Ю.... Макаров В.П. и др. Глава 9. Одесса: издание Куприенко С.В., 2017. Стр.109 - 127.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии