Методы обработки и генетической интерпретации данных дробного гранулометрического анализа
1.1. Базовые методы обработки
В настоящее время инструментарий изучения гранулометрического состава довольно разнообразен. Применяются классические ситовые наборы (для песчаных пород), лазерные и гидравлические седиментометры (для пород песчаной крупности и менее). Результатом, вне зависимости от инструментария анализа, является масса содержания каждого из классов крупности, называемых обычно фракциями. В дальнейшем объем отдельных классов выражают в процентах.
Границы фракций задаются с равным интервалом в логарифмической шкале. Это связано c фактом логарифмически-нормального распределения частиц при дроблении, доказанного А.Н.Колмогоровым [3]. В настоящее время в англоязычном научном сообщкстве при задании границ фракций гранулометрического анализа принято использовать шкалу Крумбейна [15], получившую название шкалы Ф. Основная единица шкалы вычисляется как
Ф= -log 2 d,
где d - размеры фракций в мм. При анализе шаг прогрессии обычно составляет 0,5 Ф или 0,25 Ф. В отечественной науке принято пользоваться шкалой Батурина [1] , иначе называемой шкалой гамма - γ , с шагом, равным ![]() . Значения размеров в этой шкале заменены величиной
. Значения размеров в этой шкале заменены величиной
γ = - 10 lg d,
где d - размеры фракций в мм.
1.1.1. Визуализация данных анализа
Наиболее простым и наглядным способом представления результатов гранулометрического анализа является гистограмма или график распределения массовых долей в процентах по фракциям, где по оси абсцисс откладываются средние значения размерности каждой фракции в миллиметрах (в логарифмической шкале), либо в единицах гамма или фи (т.е. в единицах, приведенных к логарифмической шкале), по оси ординат - процентное содержание каждой фракции. Обязательным условием репрезентативности данных анализа является равномерность шага границ фракций в логарифмической шкале - как правило, оно выполняется, так как принято задавать границы фракций в шкале гамма или фи. Кроме того, вместо графиков или гистограмм ранее часто приводились эмпирические полигоны распределения, где точки на графике соединялись достаточно произвольной кривой, которая строилась вручную. В настоящее время зарубежные исследователи отказались представления данных с помощью такого рода кривых , т.к. при их построении, в том числе с помощью программного обеспечения, неизбежно возникает вопрос о способе аппроксимации кривой. Достоверная аппроксимация кривых гранулометрического анализа песков возможна в случае, когда распределение близко к логарифмически нормальному, в противном случае, как справедливо было отмечено К.К.Гостинцевым [6], при аппроксимации неизбежно происходит искажение экспериментальных данных. В природных условиях идеальная схема дробления частиц, когда их распределение соответствует логарифмически-нормальному закону, осложняется условиями среды образования, где на распределение частиц обычно влияет более одного процесса.
Неочевидность построения аппроксимирующих кривых для сложных несимметричных распределений, являющихся результатом наложения влияний нескольких процессов, отмечена также в работе Новицкого и Зограф [7]. Вопрос о допустимости аппроксимаций становится критичным, когда заходит речь о выяснении генезиса исследуемых пород, поэтому и в более ранних работах, посвященных генетической интерпретации [11], и в современных работах [6] сглаживание графиков не используется.
Кумулятивная кривая традиционно применялась для определения графоаналитическими методами гранулометрических параметров (медиана, квантили, перцентили). Некоторые исследователи [13] использовали форму кумулятивных кривых для интерпретации генезиса пород.
При построении графиков, представляющих данные гранулометрического анализа, иногда возникает проблема «хвостов» распределений. В частности, при проведении ситового анализа на стандартном наборе сит с размерностью ячеек от 2 мм до 0,05 мм при наличии в образце частиц большей или меньшей размерности возникает неопределенность в определении минимального и максимального размера частиц, что не позволяет корректно построить как ЭПР, так и кумулятивную кривую. В этом случае применяется либо искусственная аппроксимация, либо столь же искусственное фиксированное назначение максимальной и минимальной размерности. С.И.Романовским [10] было предложено использовать усеченный ряд распределения частиц по фракциям - точками усечения являлись 2 мм и 0,05 мм. Во всех случаях происходит неизбежное искажение картины распределения. При построении графиков для того, чтобы показать неопределенность в «хвостах» распределения, можно оставить концы распределения открытыми, однако при вычислении коэффициентов методом моментов применение того или иного подхода к обработке открытых распределений может существенно повлиять на получаемые значения статистик.
1.1.2. Гранулометрические коэффициенты и методы их вычисления
Гранулометрические коэффициенты представляют собой величины, отражающие в обобщенном виде распределение зерен по гранулометрическим фракциям и являются частными случаями общеизвестных статистических параметров, принятых для отображения статистических коллективов. Наиболее часто они применяются для целей интерпретации в виде пар вторичных признаков - генетических диаграмм.
Наиболее часто использующиеся для интерпретации сред седиментации гранулометрические коэффициенты вычисляются методом моментов. Для исходных данных, где границы фракций указаны в логарифмических единицах (гамма или фи) используются следующие формулы вычисления среднего, стандарта, асимметрии, эксцесса и коэффициента вариации[6]:
![]()
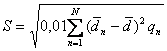
![]()
![]()
![]()
где n=1,2,...,N - номера фракций анализа, N - общее число фракций анализа, qn - относительное содержание каждой фракции в процентах к массе пробы, ![]() - среднее значение диаметра в единицах фи или гамма; S, V -стандарт и коэффициент вариации; As, Ex - асимметрия и эксцесс,
- среднее значение диаметра в единицах фи или гамма; S, V -стандарт и коэффициент вариации; As, Ex - асимметрия и эксцесс, ![]() - средний размер n-ой фракции в единицах гамма или фи:
- средний размер n-ой фракции в единицах гамма или фи:
![]()
где dn-1 и dn - верхняя и нижняя границы n-ой фракции.
Если размеры частиц представлены в миллиметрах, необходимо приведение размеров фракций к логарифмической шкале. В этом случае те же коэффициенты определяются по формулам (по [6]):
![]()
![]()
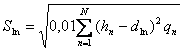
![]()
![]()
![]()
где n=1,2,...,N - номера фракций анализа, N - общее число фракций анализа, qn- относительное содержание каждой фракции в процентах к массе пробы,
![]()
dln - среднее значение диаметра в логнормальной шкале наблюдений; ![]() - среднее значение диаметра в миллиметрах; Sln, Vln - логнормальный стандарт и коэффициент вариации; As, Ex - асимметрия и эксцесс в логнормальной шкале наблюдений;
- среднее значение диаметра в миллиметрах; Sln, Vln - логнормальный стандарт и коэффициент вариации; As, Ex - асимметрия и эксцесс в логнормальной шкале наблюдений;
Данные коэффициенты вычисляются практически во всех работах, посвященных гранулометрическому анализу. Часто используемым коэффициентом является также нормированная энтропия :
![]() ,
,
где N - число фракций анализа, а H - абсолютная энтропия распределения результатов гранулометрической классификации:
![]() .
.
Помимо метода моментов, для численной оценки статистик эмпирических распределений частиц по размерам существует метод квантилей. Если метод моментов базируется на строгой вероятностной теории оценивания, то метод квантилей был разработан с целью приближенной графической оценки требуемых статистик. Значения квантилей (иначе называемых перцентилями) снимались вручную с кумулятивной кривой и затем использовались при расчете коэффициентов. Было разработано множество формул гранулометрических коэффициентов, вычисляемых с помощью метода квантилей, однако большая их часть в настоящее время практически не используется. Наиболее популярными на сегодняшний день являются коэффициенты Фолка и Варда [14]:
![]()
![]()
![]()
![]()
где Pn - n- % -ный перцентиль в миллиметрах, ![]() - среднее значение диаметра частиц, S -стандартное отклонение, As, Ex - асимметрия и эксцесс.
- среднее значение диаметра частиц, S -стандартное отклонение, As, Ex - асимметрия и эксцесс.
К коэффициентам, получаемым квантильным методом, относятся также медиана и коэффициент появления наиболее крупнозернистого класса (ПНКК, [6]). ПНКК определяется по 0,01 квантили, т.е содержанию материала в наиболее крупнозернистых классах, не превышающем в сумме 1,0% в составе песчано-алевритовой части, принятой за 100%.
Значения квантилей (перцентилей) могут быть получены путем линейной интерполяции при пошаговом (для каждой фракции) вычислении накопленных процентов по формуле
![]()
где n - процент искомого перцентиля, qi - процентное содержание фракции, k - порядковый номер фракции, в следующей за которой идет превышение искомого процента, dk и dk+1 - нижние границы размерности частиц соответствующих фракций.
Кроме того, существуют такие коэффициенты, как суммы песчаных классов, представляющие собой суммы процентных содержаний классов, границы которых берутся по той классификации, которой придерживается исследователь, могут выделяться общая сумма песчаных классов (размерность частиц 2,5-0,05 мм), сумма грубо- и среднезернистых классов (2,5-0,25 мм), сумма средне- и мелкозернистых классов (0,5-0,1), а также подсчитываться процентное содержание в гравийных, алевритовых и глинистых фракциях. Последнее существенно для того, чтобы дать правильное название исследуемому образцу.
1.1.3. Базовые методы интерпретации
Средний размер частиц является важнейшим гранулометрическим параметром. Он хорошо фиксирует положение эмпирического распределения состава на шкале размерностей и характеризует гидродинамический уровень среды седиментации. Увеличение среднего размера гранулометрического состава обломочных пород функционально обусловлено увеличением значений критерия перемещения материала осадков. Однако, в случае абсолютно несортированного осадка, хорошо сортированного осадка или осадка с бимодальным распределением средний размер может оказаться одинаковым. По этой причине средний размер обычно используется в сочетании с оценкой сортировки частиц.
Для оценки сортировки частиц по фракциям применяются стандартное отклонение, квантильные коэффициенты, коэффициент вариации и относительная энтропия.
Стандартное отклонение в общем случае пропорционально числу дробных классов, содержащих значимые количества зерен. Таким образом, становится возможной ситуация, когда осадки, сформированные в зонах активной гидродинамики, и осадки, образовавшиеся в более спокойных условиях имеют одинаковое стандартное отклонение (т.е. одинаково хорошо сортированы), что не позволяет напрямую использовать этот коэффициент для генетических реконструкций. Его используют обычно в сочетании с другими гранулометрическими характеристиками - в частности, со средним размером.
Коэффициент вариации также используется для оценки сортированности осадков. К.К. Гостинцев, основываясь на экспериментальных данных, характеризует его как дающий «более лучшую информацию о сортировке материала осадков». Им была предложена шкала для оценки сортированности по значениям коэффициента вариации из семи градаций, от 0,1-0,25 (весьма сортированный осадок) до 2,0 и более (абсолютно несортированный осадок).
Меры фракционной сортировки частиц должны учитывать характер распределения частиц по фракциям и фиксировать все фракции, в которых присутствует даже незначительное количество частиц данной размерности. В этом отношении квантильные коэффициенты уступают по информативности стандартному отклонению и коэффициенту вариации, полученном с помощью метода моментов. Однако, и квантильным, и моментным мерам сортировки может быть придан «реальный» смысл только для унимодальных кривых, для которых определены статистические приемы оценки значимости стандартного отклонения от среднего. Для бимодальных, а тем более для полимодальных кривых данные меры сортировки оказываются практически неприемлемыми. В случаях, когда в анализируемом образце имеются частицы песчаной, алевритовой и глинистой размерности, наличие дефицитов на рубеже этих совокупностей предопределяет появление локальных минимумов кривой распределения и, как следствие этого, би- и полимодальность кривой [9] . Локальные минимумы могут наблюдаться также и в образцах, сложенных исключительно частицами песчаной размерности. Коэффициентом, применимым для оценки би- и полимодальных распределений, является нормированная (или относительная) энтропия, зависящая только от дробности гранулометрического анализа и выбранной масштабной шкалы. Зависимость от шкалы, однако, делает затруднительным сопоставление данных анализа, полученных с применением разных масштабных шкал. С.И. Романовским была разработана равномерная шкала классификации осадков по степени сортировки на основе энтропийного принципа оценки сортировки [10]. Благодаря использованию нормированной энтропии в этой классификации возможно выделение крайних членов - идеально сортированный осадок (Hr=0) и абсолютно несортированный осадок (Hr=1).
Асимметрия и эксцесс, как и упомянутые выше моментные и квантильные меры сортировки, также пригодны лишь для оценки унимодальных кривых. Параметр асимметрии дает информацию о результатах взаимодействия процессов дифференциации и интеграции различных ассоциаций обломочных частиц песчано-алевритовой размерности.
Положительные значения асимметрии показывают, что модальный размер в эмпирическом распределении больше среднего размера гранулометрического состава. В таких распределениях преобладают классы с большой размерностью частиц, а тонкозернистые составляют так называемые «хвосты» распределений. В случае отрицательной асимметрии модальный размер меньше среднего размера гранулометрического состава. При таком распределении преобладают тонкозернистые классы, а более крупнозернистые составляют его «хвост». В симметричных распределениях модальный и средний размеры равны. Чем больше абсолютное значение отрицательной асимметрии, тем лучше отсортированы тонкозернистые классы по сравнению с более крупнозернистыми. Наоборот, чем больше абсолютное значение величины положительной асимметрии, тем лучше отсортирован крупнозернистый материал.
Исследование гранулометрического состава современных песчано-алевритовых осадков К.К.Гостинцевым позволило выявить различные комбинации привноса и выноса материала той или иной размерности, сильно влияющего на асимметрию его распределения. Например, положительная асимметрия образуется при обильном привносе материала крупнозернистых классов. Такая же асимметрия возникает при обильном привносе в осадок тонкозернистого материала, в результате модальный размер становится меньше среднего размера. Одновременный привнос крупнозернистого материала и вынос тонкозернистого, как правило, приводит к увеличению моды и приводит к образованию симметричных распределений гранулометрического состава преобразованных осадков.
Мера эксцесса характеризуется степенью выпуклости кривой распределения. При эксцессе, равном нулю, кривая распределения совпадает с логнормальной кривой. Пикообразность кривой свидетельствует о том, что модальный и смежные классы характеризуются повышенным процентным содержанием материала. Положительные значения эксцесса указывают на стабильность переработки и пересортировки обломочного материала на относительном уровне, определяющимся средним размером диаметра зерен. Значительный по величине положительный эксцесс указывает, что либо в короткий период времени действовали эоловые или гидродинамические процессы, либо слабые процессы действовали в течение длительного периода. В любом случае, скорость динамической обработки (сортировки) привносимого обломочного материала превышала интенсивность его привноса.
Отрицательные значения эксцесса указывают на то, что привнос обломочного материала значительно превышает интенсивность его динамической переработки. Например, привнос обломочного материала и осаждение его в динамически застойных условиях характеризуется отрицательными значениями эксцесса. Гранулометрический состав осадков коры выветривания выражен отрицательным эксцессом, обычно от -0,4 до -1,0 [6].
Если интенсивность привноса обломочного материала и скорость динамической переработки были в равновесном состоянии, то эксцесс характеризуется нулевыми значениями.
Коэффициент появления наиболее крупнозернистого класса указывает на максимальный размер зерен в составе того или иного осадка и заключает в себе много ценной информации относительно источников сноса и путей перемещения обломочного материала в бассейнах седиментации. Наибольшие значения коэффициента прямо пропорциональны ухудшению сортировки материала осадков. Путем картирования выявляют частоту встречаемости тех или иных значений коэффициента по площади и в разрезах. Направление возрастания встречаемости наибольших значений указывает на источник сноса обломочного материала.
1.2. Методы генетической инетпретации
1.2.1. Генетические диаграммы.
Содержательной основой всех генетических диаграмм является положение о том, что гранулометрический состав осадков формируется под действием динамики среды осадконакопления, а каждой обстановке гранулоседиментогенеза присущи свойственные только ей особенности динамического режима, соответственно, имея в своем распоряжении конечный продукт седиментации - гранулометрические анализы осадков, можно восстановить и динамику среды, и саму обстановку восстановления осадков. Усилия геологов, как правило, ориентировались на поиск универсальных характеристик фракционного состава, призванных разделить осадки разных типов.
Одной из первых популярных генетических диаграмм была диаграмма Л.Б.Рухина [11]. Реализованный в ней подход заключается в использовании для установления генезиса песчаного осадка двух коэффициентов - среднего размера и коэффициента сортировки (стандартного отклонения). В основе метода -динамическая диаграмма, эмпирически найденная путем анализа нескольких сотен образцов современных осадков. На диаграмме выделяются 5 полей:
-поле песков, отложенных а неподвижной или ламинарно-движущейся воде, характеризующихся малыми значениями обоих коэффициентов.
-поле песков, осажденных при колебательных турбулентных движениях воды, в прибрежной части бассейнов. Характеризуются высокими средними размерами и хорошей сортировкой.
-поле песчаных осадков, отложенных в однонаправленном турбулентном потоке. Средний размер варьирует в широких пределах, сортировка хуже, чем в двух предыдущих случаях
-поле эоловых песков характеризующееся высокими средними размерами и плохой сортировкой осадка.
-поле недостоверности, в которое попадают породы с низкими значениями средних размеров.
Данная диаграмма многократно подвергалась критике [9,10,12]. Некоторые исследователи строили свои варианты генетических диаграмм на основе коэффициентов среднее - стандартное отклонение [16]. Метод Рухина, в сущности, является одним из многих вариантов перебора разных комбинаций гранулометрических коэффициентов с целью получения генетической интерпретации, причем перебор характеристик часто производился «вслепую», без учета физического смысла тех или иных коэффициентов (к примеру, в работах Саху [18] использование определенных сочетаний коэффициентов оправдывается тем, что исходные данные анализа лучше всего ложатся на диаграмму именно с этими коэффициентами). По оценке С.И.Романовского [9], ни одна из подобных диаграмм не выдерживает критики, так как они работают только на материале автора диаграммы. В целом, можно сказать, что использование произвольных сочетаний коэффициентов допустимо для диверсификации схожих пород или осадков, однако генетическая интерпретация по ним затруднительна даже в том случае, если коэффициенты применены корректно (т.е. если распределения близки к логнормальному).
Другой подход к генетическим диаграммам имеет в свой основе осознанный выбор тех коэффициентов, которые отражают динамику природных процессов. В первую очередь следует рассмотреть диаграмму Пассеги [17], пожалуй, на сегодняшний день наиболее известную в мире.
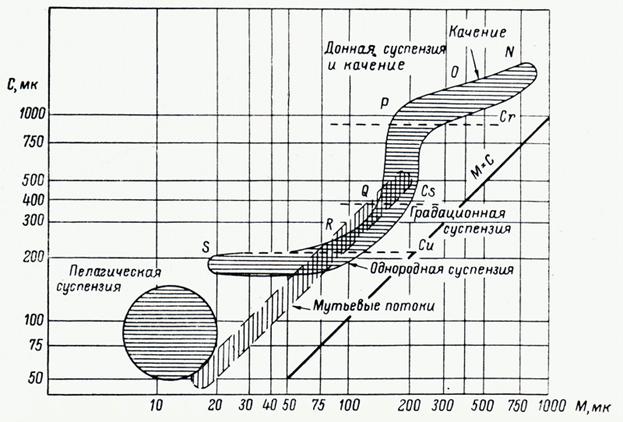
В основе метода Пассеги лежит представление о том, что перенос осадка в движущемся потоке осуществляется: во-первых, путем качения по дну, во-вторых, путем влечения в неоднородной суспензии, где нижние части обладают большей плотностью по сравнению с верхними, в третьих, путем перемещения в однородной суспензии. Соотношение между методами определяется динамикой потока. На диаграмме Пассеги по осям откладываются средний размер M и 1%-ный квантиль С, который должен характеризовать максимальную подъемную мощность потока, и выделяются следующие поля: пелагическая суспензия (осадки «спокойной воды»), мутьевые потоки, однородная суспензия, градационная суспензия, донная суспензия и качение (рисунок) - то есть как таковая привязка к обстановке осадконакопления отсутствует, рассматривается только механизм переноса частиц, на основе которого можно сделать предположения об обстановке осадконакопления. Эоловые отложения не рассматриваются. Поля на диаграмме Пассеги отличаются разной степенью достоверности, в том числе и за счет того, что они перекрывают друг друга.
Генетические диаграммы асимметрия-эксцесс построены на принципе механической дифференциации песчано-алевритовых частиц в различных фациальных условиях. К ним относятся диаграммы Г.Ф.Рожкова [8] и К.К.Гостинцева. Основное отличие этих диаграмм - в том, что в первой при получении коэффициентов используются количественные проценты содержания зерен во фракциях, во второй - общепринятые весовые проценты.
На диаграмме Гостинцева, составленной на основе анализа более 1000 проб современных осадков, выделяемые области носят название динамогенетических полей, соответствующих той или степени механической дифференциации обломочных частиц.
Поле 1 (Эксцесс > 7, асимметрия отрицательная) характерно для эоловых осадков. При этом чем больше значение эксцесса и меньше абсолютное значение асимметрии, тем большую зрелость имеет осадок (скорость динамоэоловой пересортировки превышает скорость привноса обломочного материала).
Поле 2 (Эксцесс от 7 до 4, асимметрия отрицательная) - эоловые и пляжные осадки. Наиболее характерны фации пологих пляжей, сильный накат волн, эоловая переработка материала на пляже, эолово-морские микрофации, эоловые валы на пляжах равнинных рек, эоловые вдольбереговые дюны, передовые прибрежные валы в зоне наката-отката волн.
Поле 3 (Эксцесс от 4 до 2, асимметрия отрицательная) - эолово-морские осадки, сформированные в результате выдувания тонкого материала из пляжных и эоловых осадков береговых дюн и отложением его в прибрежной зоне подводного склона морского пляжа; осадки морского пляжа в зоне наката-отката волн; осадки эоловых образований разного типа (линзы, пересыпи, валы) на поверхности пляжа в периоды между сильными штормами; осадки пляжей крупных равнинных рек, озер.
Поле 4 (Эксцесс от 2 до 0, асимметрия отрицательная) - эоловые осадки отсутствуют, характерны фации побережья вдоль береговой линии, фации мутьевых потоков, русловые осадки рек с сильным течением, фации пляжей вдоль размываемых берегов заливов крупных озер, заливов и крупных равнинных рек.
Поля 5 и 6 (с отрицательными значения эксцесса) характеризуются, как правило, осадками с би- и полимодальными кривыми распределения частиц по фракциям. За счет этого разделение этих осадков по параметрам асимметрия-эксцесс невозможно (фактически здесь мы опять сталкиваемся с «полем неопределенности»), хотя для поля 6 (с положительной асимметрией) предложен генезис осадков как осадков слабых течений, застойных зон, озер и кор выветривания.
Поле 7 (Эксцесс 0-2, положительная асимметрия) - фации широких участков устьев рек, участков мелководья, речных плесов, морские фации, континентальные фации в зоне разрушения мелкокристаллических магматических и мелкозернистых осадочных пород. С увеличением асимметрии становятся более характерны морские фации.
Поле 8 (Эксцесс 2-4, положительная асимметрия) - осадки рек и пойм, с увеличением асимметрии становятся более характерны морские осадки.
Поле 9 (Эксцесс 4-7, положительная асимметрия) - осадки, дифференциация обломочного материала которых обусловлена активным волновым воздействием при ослаблении роли поступательного движения воды - течений. При асимметрии более 1,0 более характерны осадки зоны выхода волн на мелководье открытых бассейнов, при меньших значениях - осадки широких устьев рек и проток дельт.
Поле 10 (эксцесс более 7, положительная асимметрия) - осадки, характеризующие активный волновой режим с периодическим влиянием приливно-отливных явлений, которые обуславливают перенос и осаждение мелкозернистого материала из взвешенного состояния. Штормовыми волнениями донный осадок взмучивается, а более тонкий материал выносится в более глубокую часть бассейна. Данный процесс напоминает эоловый с тем отличием, что в водной среде взвешивание материала или его поддержание его во взвешенном состоянии обуславливается штормовыми волнениями.

Таким образом, данная диаграмма, основанная на динамогенетической интерпретации коэффициентов асимметрии и эксцесса, также не всегда позволяет вполне однозначно говорить о генезисе породы. Кроме того, ее применение для анализа отложений с би- и полимодальным распределением частиц по фракциям некорректно и приводит к попаданию в «поле неопределенности».
Анализ эмпирических полигонов распределения (метод Б.Н.Котельникова)
По известному выражению Таннера [19] , гранулометрические коэффициенты "маскируют столько же информации, сколько ее предоставляют". Альтернативным методом генетического анализа гранулометрических данных является их интерпретация без использования гранулометрических коэффициентов. Подход к генетической интерпретации без использования генетических диаграмм предполагает анализ самих распределений, изображенных графически.
Попытка систематизировать анализ графических изображений была сделана Д.Дугласом [13].По мнению Дугласа, соотношение частиц, влекомых потоком, зависит от состава коренных пород и скорости потока на всем его протяжении. Если бы весь транспортируемый материал мог отложиться одновременно в момент внезапного прекращения течения, то осадок обладал бы распределением частиц, совпадающим с распределением их в суспензии. Поскольку, однако, подобной остановки течении не происходит, в той или иной точке на дне потока, в зависимости. от его динамики, может быть отложена какая-то часть влекомого осадка, обладающая определенной кривой распределения. Дугласом было выделено три основных типа гранулометрических кумулятивных кривых, связанных со скоростью потока, а реальные кривые рассматривались как сочетание граничных вариантов. Было выделены типичные сочетаний базовых кривых, позволяющие выделять 7 обстановок осадконакопления: аллювиальный комплекс, озерные отложения, морские и озерные дельты, низины, заливаемые приливами и мелкоморье, береговые пески, неритовые и. абиссальные области, эоловые пески. Этот метод мало использовался и не получил сколько-нибудь надежного подтверждения. Одной из причин малой популярности метода является его очевидная субъективность - в основе метода лежат визуальные наблюдения кривых и их градация по принципу «похоже - не похоже», хотя сравнительный визуальный анализ кривых распределения до сих пор часто применяется в исследованиях, касающихся данных из одного региона или одной группы генетических типов отложений.
Методика Б.Н.Котельникова [4] основана на детальном анализе ЭПР более 1300 образцов песков. Ее автор не использовал гранулометрические коэффициенты, так как большинство статистических параметров пригодны для описания нормального (логнормального) или близких к нему распределений, преобладающих в природе, но не исчерпывающих их разнообразия. Использование этих параметров для отражения сильно деформированных нормальных распределений, распределений, подчиняющихся другим законам, а также бимодальных совокупностей, являющихся смешением простых субраспределений, некорректно.
В большинстве случаев трансформация распределения при транспортировке определяется рядом явлений. Б.Н.Котельниковым был сделан вывод, что каждому способу транспортировки соответствует свое логнормальное распределение. Им были сформулированы следующие ограничения для правил идентификации субаквальных песчаных распределений:
-скорости частиц, перемещающихся разным способом, можно выразить в виде следующего неравенства: V потока>V взвеси>V сальтации>V качения.
- нижняя граница для сальтации устанавливается около 100 мкм. Зерна меньшего размера при исследовании оказываются совершенно неокатанными, часто вблизи этого интервала наблюдается дефицит частиц.
-нижняя граница качения устанавливается в интервале 250-300 мкм (частицы такого размера характеризуются минимальными срывающими скоростями, а теоретически движение частиц начинается с качения). Зерна более мелкие (100-250 мкм) начнут перемещаться сальтацией, а еще более мелкие сразу перейдут во взвесь.
- верхняя граница частиц, транспортирующихся различными способами, не может быть установлена, так как зависит главным образом от скорости и турбулентности потока (грязевые потоки, штормовые волны и пр.). Также неопределенной остается граница взвесей, уходящая в область алевритов и пелитов.
С учетом этих ограничений были сформулированы правила идентификации субаквальных песчаных распределений:
1) в интервале 0,05-2 мм может иметь место трехвершинное распределение, отвечающее трем видам транспортировки (взвеси, сальтации, качению). Однако при стационарном режиме отложения, который наблюдается в подавляющем большинстве случаев, резко преобладает объем только одного распределения: взвешенных или сальтирующих частиц. Для частиц размером менее 2 мм качение не может быть доминирующим способом транспортировки.
2) 2-вершинное распределение может отвечать только сальтации и взвеси, т.к. взвесь и качение не могут сосуществовать без сальтации, также как не может быть сальтации и качения без захвата взвешенных частиц. Однако известны случаи, когда влияние слабых придонных течений на ранее отложенный из взвеси осадок приводит к возникновению аномальных двухвершинных распределений: основное обусловлено взвесью, дополнительное, грубозернистое - качением.
3) одновершинное распределение может соответствовать только взвеси, .т.к. при отложении сальтирующих или же катящихся частиц имеет место «гидравлический захват» более мелких частиц более крупными.
4) Многовершинные распределения чаще всего отвечают осадкам, отложенным из среды повышенной плотности за счет смешения разных структурных типов осадков и изменения верхней размерной границы взвешенных частиц при пульсационных изменениях скорости потока (грязевые потоки, пролювий). В грубозернистых аллювиальных осадках при гетерогенной транспортировке многовершинные распределения возникают не только за счет быстрого изменения верхней размерной границы взвешенных частиц, но и за счет изменения соответствующих границ сальтирующих и катящихся частиц.
5) В воздушной среде, в отличие от водной, распределения сильно растянуты по размерной шкале и редко перекрывают друг друга.
Метод Б.Н.Котельникова разрабатывался на основе анализов только песчаной составляющей, и для распределений, «открытых» в тонко- или грубозернистой части, были рассмотрены следующие варианты:
-распределение открыто в тонкозернистой части. Это вызвано тем, что тонкозернистый материал достаточно инертен и не дифференцируется в водном потоке. Генетически такое распределение может быть интерпретировано по песчаной части осадка.
-распределение открыто в грубозернистой части. Требует детального анализа крупнозернистого материала, анализ песчаной составляющей не дает значимого результата.
-распределение открыто в и в тонко- и в грубозернистой части, осадок очень плохо сортирован. Для интерпретации достаточно знать характер песчаного распределения и объем тонко- и грубозернистых фракций.
На основе этих принципов, путем анализа ЭПР выделялось следующие типы и подтипы песков:
1. Элювиально-делювиальные, неперемещенные вулканогенные и моренные осадки
2. Делювиально-пролювиальные, перемещенные моренные осадки
3. Стрежневые аллювиальные пески
4. Аллювиальные русловые пески
5. Прибрежно-морские пески пляжа и подводных аккумулятивных форм (2 подтипа -пески пляжа и пески подводных береговых форм)
6. Пески речных пойм и морские пески области слабой волновой переработки (2 подтипа - донные пески и пески, образующиеся при мгновенной разгрузке взаешенных частиц)
7. Эоловые пески (2 подтипа - перемещенные и остаточные)
В работах Б.Н.Котельникова подробно рассмотрены особенности кривых каждого типа. К основным критериям, позволяющим отнести исследуемый образец к тому или иному типу, относятся такие параметры, как модальность распределения, размерность моды (или мод субраспределений), симметричность распределения (субраспределений), количество грубых и тонких фракций («открытость» распределения), соответствие частей распределения логарифмической функции, объемы субраспределений, четкость дефицитов субраспределений, сравнительные характеристики серий однотипных ЭПР.
Глава из магистерской работы администратора данного сайта. На мой взгляд, может быть полезна компактным изложением основных методик. Список источников приведен ниже.
По этой же теме: Обработка данных гранулометрии online
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии
Комментарии
Спасибо,
Спасибо, Тимофей!
Хоть и в сжатой форме, но все основное есть)))
Уважаемый, Тимофей
Уважаемый, Тимофей Александрович!
Выложите, пожалуйста, список литературые по этой статье.
Заранее благодарю!
Литература
19.Tanner W.F. Modification of sediment size distributions.// J.Sediment.Petrol., 1964, vol.34, N 1, p.156-164.
Вопрос Тимофей
Вопрос
Тимофей Александрович, поясните, пожалуйста.
При обработке гравелитов и конгломератов мы разделяем их на 15 фракций. Но в общем объёме встречаются песчаные отложения, в которых фракции >2 мм содердат по несколько обломков общей массой близкой к нулю. Таким образом, получается в единичных случаях, что в расчете не 15 фракций, а 11 или даже 10.
Вопрос 1: если в расчет нормированной энтропии мы обычно записываем 15 фракций, то как поступать с в единичных случаях? Так же и считать по 15 для валового расчета или индивидуальный подход и писать 11?
Вопрос 2: как поступать если много проб, у которых эксцесс варьирует в пределах (-1,1)-(-1,74) и 6,1-9,4? Расчет ведется с использованием Фи.
1. Все зависит от цели, с
1. Все зависит от цели, с которой рассчитывается энтропия. Если хотим сравнить степень сортированности всех отложений (и песков, и конгломератов, и песков с большой гравийной составляющей), то считаем с учетом всех 15 фракций. Если первые фракции пусты - значит осадок лучше сортирован. Соотвественно, чистые пески будут иметь показатель нормированной энтропии меньше, чем пески с гравием итд. А если хочется сравнить отдельно одни пески с другими - можно, конечно, и не учитывать первые пустые фракции. Тогда относительная энтропия для них получится больше, ее можно будет использовать только для сравнительного анализа тех проб, где расчет велся для 11 фракций.
2. Не важно, в какой шкале ведется расчет асимметрии и эксцесса, эти характеристики не зависят от того, используется ли при расчете фи, гамма, натуральные логарифмы или любая другая логарифмическая шкала. Но могут завсеть от размера шага в самом наборе фракций. Если, например, шаг - Ф/2, то значения эксцесса могут отличаться (от тех, например, с которыми работал Гостинцев) за счет огрубления - в одну фракцию Ф/2 попадают почти две фракции гамма.
Как поступать - не знаю. Получается, что у Вас все ЭПР сводятся к двум типам - очень высокой степени сортировки и практически несортированные? Видимо, большие значения эксцесса там, где почти все попадает в гравийные фракции, а отрицательные - там, где пристутствует и гравий, и песок?
Спасибо за разъяснения! Вот
Спасибо за разъяснения!
Вот за такие сложные задачи решили мы взяться.
Вот только не понятным остается, когда эксцесс варьирует 9,2-9,4 при количестве фракций крупнее 2 мм в сумме не больше 10 %. Как Вы смотрите на такое. Может у нас где-то закрадывается ошибка?
Может быть, действительно
Может быть, действительно есть где-то ошибка в расчетах. Можете прислать исходные данные и полученные коэффиценты для одного из образцов, вызывающих сомнение, проверю.
Проблема
Тимофей Александрович, я не имею представления как Вам выслать исходные данные. Как узнать Ваш электронный адрес. Где такие данные хранятся?
Здравствуйте, Тимофей
Здравствуйте, Тимофей Александрович!
Я региональный нефтяной геолог. Мы восстанавливаем обстановки осадконакопления в основном по ГИС(ам).
Хотелось бы использовать и гранулометрический анализ. Кернового материала немного, колличество выделенных фракций максимально 8 и 15 (по 2 местороджениям) в остальных - по 5 (чувствительности никакой). Из литературы только Рединг и Романовский :(
Есть ли возможность связаться с Вами, для получения консультаций?
С уважением, Эльвира
Косвенный пересчет
Везде дискутируется вопрос графического получения данных от квартилей разных процентов. А Рожков. Г.Ф. вообще считал (почти в каждой статье), что косвенный пересчет - самый лучший метод.
Как быть?
Однако, гранулометрический
Однако, гранулометрический анализ, в том виде, в котором существует, метод сильно некорректный (см. того же Романовского и Гриффитса) и может использоваться только для решения самых общих задач типа: отличается ли один осадок от другого. И не более. Основная причина - использование абстрактного понятия "размерный класс" и отсутствие вещественного наполнения этого класса. Т.е. косвенному измерению (а все предлагаемые методы - косвенные, включая последние разработки типа лазерных гранулометров и основанных на видеоизображениях анализаторов) подвергается материал смешанного состава (в состав анализируемой смеси входит серия минералов и полиминеральных зерен с различными физическими характеристиками).
Правильно написал Гриффитс - мерять надо мономинеральную фракцию, каждое зерно, по трем размерам и прямым измерением и в ненарушенном материале. Тогда только можно зацепить какие-то особенности гидродинамики, в которой осадок формировался.
О КАЧЕСТВЕ ГРАНУЛОМЕТРИЧЕСКИХ ИНТЕРПРЕТАЦИЙ.