Нефть. Новые свойства: возгоны и полиномиальные уравнения
Макаров В.П.
НЕФТЬ. НОВЫЕ СВОЙСТВА: возгоны и полиномиальные уравнения.
Российский государственный геологоразведочный университет, Москва.
Введение.
Проведённые ранее исследования [1, 2] с применением корреляционного анализа показали широкое развитие в нефтях линейной зависимости (до 99% объектов) между компонентами состава нефти, в частности, d – n – физические свойства нефти, С-Н (химический состав нефти), Сm-Hn (молекулярные содержания элементов), параметры группового состава - Нф (нафтены), Мн
|
Уравнение связи
|
R²
|
Количество выборок
|
%%
|
||
|
Общее
|
под-видов
|
разновидностей
|
|||
|
МН1 = -34,73НФ + 54,18
|
0,882
|
83(?)
|
53
|
|
63,90%
|
|
МН11 = -34,43НФ + 58,37
|
0,832
|
|
24
|
45,30%
|
|
|
МН12 = -38,57НФ + 41,71
|
0,977
|
|
10
|
18,90%
|
|
|
МН13 = -46,34НФ + 41,50
|
0,983
|
|
16
|
30,20%
|
|
|
МН2 = -29,80НФ + 42,16
|
0,978
|
11
|
|
36,10%
|
|
|
АР1 = -23,28НФ + 12,40
|
0,938
|
38
|
26
|
|
68,40%
|
|
АР2 = -28,38НФ + 25,41
|
0,951
|
9
|
|
31,60%
|
|
|
АР1 = -57,58МН + 18,08
|
0,919
|
26
|
15
|
|
57,70%
|
|
АР2 = -43,18МН + 11,78
|
0,984
|
8
|
|
42,30%
|
|
компоненты). Эти зависимости приведены в (табл.). В редких случаях найдена зависимость, представленная на рис.1. Она отражает связь между Нф и Ар, которая описывается уравнением Ар = -1,4812(Нф)2 + 4,1584(Нф) - 1,0284 и имеет вид 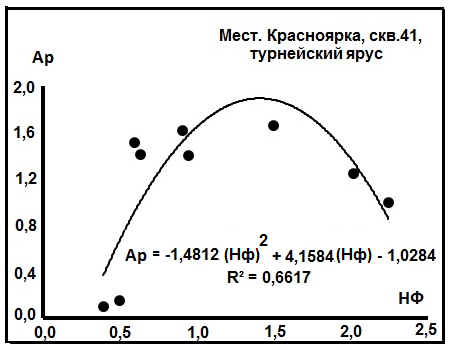
полиномиального, или параболического (квадратичного), уравнения y = Ax2 + Bx + C. Подобные вещи описывает А.И.Брусиловский [10], рассматривая зависимость от Т парных взаимодействий между газами, например, N-H2S, H2S-CH4, CH4-C2H6 и др. Таких оказалось всего 7 из 89 пар. Этот результат говорит о возможном распространении в природе полиномиальных распределений геологических компонентов. Видимо, впервые, этот факт был установлен при изучении распределений изотопов в минералах. Наиболее близки этой ситуации уравнения фракционирования изотопов лёгких элементов (O, С и пр.). Например, для распределения изотопов кислорода между кварцем и водой это уравнение имеет вид lnα(SiO2-H2O*) = 1,92·106/T2 + 8,58·103/T - 18,98 (J.Kawabe, 1978), представляющее типичное полиномиальное (параболическое) уравнение (полиномы) второго порядка. Этим же путём пошёл и В.Б. Поляков [7]. Оценка этих приёмов приведена в [8]. Частично эти результаты отражены в работе [2] на примере месторождения Озек-Суат [4]. На рис. 2 представлены также материалы и по другим объектам. Были и более редкие случаи: в одной выборке дегазированной нефти [10, табл. 12.2] фиксировались по два полинома – см. рис. 3.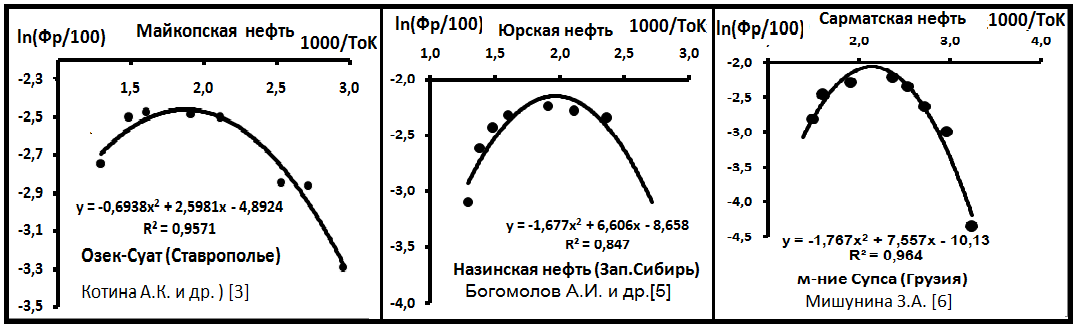
Рис.2. Динамика получения возгонов на месторождениях нефти.
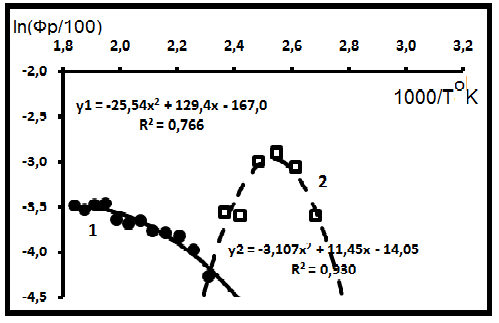
Рис.3. Динамика получения возгонов из дегазированной нефти [10].
В связи с этим, были изучены зависимости от температуры количеств возгонов по опубликованным данным. Результаты этих исследований вынесены в табл.1 (X=1000/ToK, Y= ln(Фр/100); Фр – количество нефти в возгоне (во фракции) в %). В табл.1 отмечены анализы проб до отделения ароматики – индекс «да», и после отделения ароматики – индекс «па». Недостатком этих исследований является отсутствие данных при T> 550оС. В большинстве месторождений изучены короткие интервалы температур получения возгонов, как правило, до 300оС.
Свойства полиномиальных (параболических) уравнений.
Полученные данные свидетельствую о широком распространении в геологической среде полиномиальных уравнений вида
y = Ax2 + Bx + C. (1)
Свойства же их изучены недостаточно. В реальной ситуации множество
|
№№ п.п.
|
Месторождение
|
Воз-раст
|
Параметры уравнения y=Ax2+Bx+C
|
Регион
|
Источник
анализов
|
|||
|
A
|
B
|
C
|
A’
|
|||||
|
1
|
Супса.
|
N
|
-1,767
|
7,667
|
-10,130
|
-1,2315
|
Грузия.
|
[6]
|
|
2
|
Чаладиди
|
K
|
-0,788
|
2,517
|
-4,469
|
-0,976
|
Грузия.
|
[6]
|
|
3
|
Озек-Суат, скв.69, да
|
K
|
-2,655
|
10,65
|
-12,98
|
-1,165
|
Ставрополье.
|
[4]
|
|
4
|
Озек-Суэт, скв.69, па
|
K
|
-2,476
|
9,501
|
-10,97
|
-0,7345
|
Ставрополье.
|
[4]
|
|
5
|
Озек-Суэт, скв.42, да
|
J
|
-1,12
|
3,946
|
-5,644
|
-0,849
|
Ставрополье.
|
[4]
|
|
6
|
Озек-Суэт, скв.42, па
|
J
|
-1,846
|
6,282
|
-7,748
|
-0,733
|
Ставрополье.
|
[4]
|
|
7
|
Назинская нефть
|
J
|
-1,677
|
6,606
|
-8,658
|
-1,026
|
Зап.Сибирь.
|
[5]
|
|
8
|
Назинская нефть
|
J
|
-2,041
|
7,551
|
-9,19
|
-0,8195
|
Зап. Сибирь.
|
[5]
|
|
9
|
Красноярка, скв.42
|
C
|
-1,974
|
7,389
|
-9,373
|
-0,992
|
Волго-Урал.
|
[3]
|
|
10
|
Красноярка, скв. 41.
|
C
|
-1,061
|
3,964
|
-6,137
|
-1,0865
|
Волго-Урал.
|
[3]
|
|
11
|
Краснокамское
|
C
|
-1,704
|
8,556
|
-13,78
|
-2,612
|
Волго-Урал.
|
[9]
|
|
12
|
Зольный Овраг, скв. 69.
|
C
|
-1,148
|
4,6
|
-6,951
|
-1,1755
|
Волго-Урал.
|
[3]
|
|
13
|
Зольный Овраг, скв. 87.
|
D
|
-1,012
|
4,451
|
-7,191
|
-1,37
|
Волго-Урал.
|
[3]
|
|
14
|
Сепарированная нефть
|
|
-1,226
|
6,251
|
- 9,856
|
-1,8025
|
|
[10]
|
параметров линейных уравнений обобщаются с помощью компенсационных уравнений. Поэтому параметры полиномиальных уравнений также были подвергнуты компенсационному анализу.
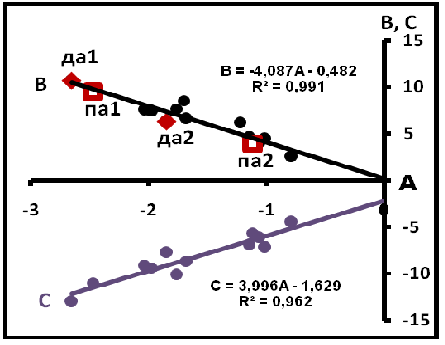
Рис. 4. Надкомпенсационные уравнения по параметрам полиномиальных (параболических) уравнений второго порядка.Результаты отражены на рис.4, который показывает, что эти условия выполняются, соответствующие уравнения имеют вид (2) и (3) и представлены на рис. 4.
Эти данные говорят о том, что какой бы ни была нефть, между параметрами параболического уравнения существует устойчивая линейная связь. Уравнения подобного типа названы надкомпенсационными (или просто надкомпенсацией). На диаграмму рис.4. вынесены также точки да и па для двух проб. Для удобства анализа они обозначены цифрами 1 и 2 (да-1, да-2 и па-1, па-2), а точки выделены цветом. Как показывает сопоставление, эти точки, перемещаясь вдоль надкомпенсации, нигде не выходят за её пределы. В особых точках, которыми мы называем точки пересечения кривых, параболические уравнения можно преобразовать в квадратичные уравнения. Действительно, в этих точках y1 = y2; тогда две параболы объединяются в параболу (A2-A1)x2 + (B2-B1)x + (C2-C1) = 0 или
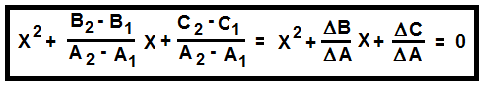
Cравнение коэффициентов в этом уравнении с параметрами надкомпенсаций на рис.3 показывает, что статистически первые - это угловые коэффициенты соответствующих надкомпенсаций (рис.4), поэтому можно записать:
x2 + mx + k =0. (4)
Наконец, анализ табл.1 показывает, что параметры A, B и C связаны ещё соотношением 2A ≈ В + С ((см.столбец А’).
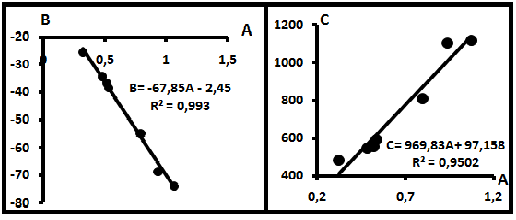
Рис.6. Надкомпенсационные уравнения для теплоёмкостей твёрдых веществ [13].
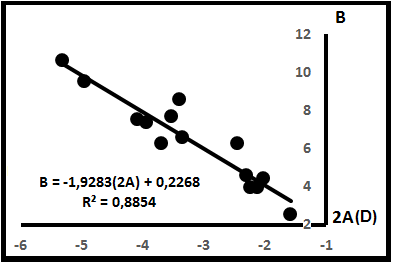
Для раскрытия смысла надкомпенсаций найдём первую производную по x уравнения y=Ax2+ Bx +C, имеющая вид 1/(Фр/100) = 100/Фр = 2Ax + B. На рис. 5 приведена компенсационная диаграмма по параметрам производных.Сопоставление показывает аналогию между ними. Производные описываются уравнениями прямых линий, и эти прямые пересекаются, согласно [11], в точке с параметрами Do =(2Ао) = 1,928 и Bo = 0,227.
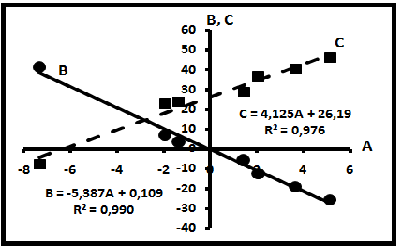
Рис.7. Надкомпенсационные уравнения для теплопроводностей сталей [14].
Для проверки широты распространения этих свойств полиномов рассмотрим удельную теплоёмкость твёрдых веществ [13] и теплопроводность сталей [12, табл. 1.4]. Физические свойства всех этих веществ хорошо описываются полиномиальными (параболическими) уравнениями второй степени y = Ax2 + Bx + C, для них были определены постоянные А, В и С и вид связи между ними, показанные на рис. 6, 7. Что касается материалов А.И. Брусиловского [10], то в его условиях уравнения надкомпенсации не получены, поскольку, видимо, среди этих пар газов были разнородные элементы. Согласно [10] с ростом температуры возгона происходит рост молекулярного веса и стандартной плотности возгона (см. табл.2) [10,таб.6.4].
|
Температурные пределы отбора фракции, °С
|
Выход на нефть, %.
|
Плотность при стандартных условиях, кг/м3
|
Молярная масса,
г/моль
|
|
НК-60
|
8,7
|
640,9
|
|
|
60-95
|
12,9
|
698,7
|
|
|
95-122
|
10,9
|
726,8
|
|
|
122-150
|
7,4
|
740,4
|
|
|
150-200
|
15,2
|
760,8
|
|
|
200-250
|
13,5
|
813,3
|
169
|
|
250-300
|
10,3
|
828,4
|
186
|
|
300-350
|
6,3
|
841,5
|
202
|
|
350-400
|
4,8
|
|
248
|
Таким образом, сопоставление всех этих данных показывает наличие у них такого свойства как надкомпенсация. Более-менее чёткий смысл имеет надкомпенсация (А – В), и он связан с компенсациями первых производных к этим полиномам. Близкий смысл имеет надкомпенсация (В – С). Она связана с первой производной по x уже полинома третьей степени y =Ax3 +Bx2 +Cx+D. Смысл надкомпесации (А – С) не ясен.
Координаты точек пересечения полиномов.
Поскольку обычно изучаются полиномы нескольких нефтяных объектов, то правомерен вопрос об их пересечениях (так называемые отмеченные выше особые точки), координатах этих точек и их физическом смысле. Основным свойством этих точек является принадлежность их одновременно всем кривым.
Исходное уравнение имеет вид y = Ax2 + Bx + C, согласно (4) кривая, проходящая через общую точку пересечения (xo, yo) –
xо2 + mxо + k =0.
Для конкретных нефтяных объектов (см. рис.3) m = -4,087 ≈ 4; k = 3,996 ≈ 4. Дискриминант этого уравнения D=B2-4AC преобразуется в D = m2-4k (при А = 1) ≈ 0. Поэтому это уравнение в первом приближении имеет один корень xo = -m/2 ≈ 2. Уравнение, проходящее через общую точку (xo, yo) имеет вид
yo = Axo2 +Bxo + C. (5)
Преобразуя (5) с учётом (2) и (3), получаем B =-A(xo2 + k)/xo - K/xo +yo/xo и после сравнения его с (2) и (3) имеем
m = -(xo2+k)/xo; M = -K/xo+yo/xo. (6)
Преобразуя эти равенства, приходим к решению задачи о координатах точек пересечения полиномов (парабол):
Здесь k, K – постоянные и известные величины (параметры уравнений надкомпенсаций). Отсюда
yo = -0,482∙2 -1,629 = -2,593.
С учётом этих данных имеем:
Физический смысл значений xo и yo не ясен.
Интерпретация полиномиального (параболического) уравнения.
ln(Фр/100) ≈ -[A(1/T – 1/То)2]+ В. (8)
Интерпретация этого уравнения возможна в двух направлениях.
1). Согласно существующим точкам зрения «уравнения параболического типа описывают процессы … диффузии (движение частиц среды, приводящее к переносу вещества и выравниванию концентраций) и определяются условием B2 − 4AC = 0» [15] . Поскольку в данном случае рассматривается воздействие только одного параметра (температуры), то уравнение диффузии приобретает вид [15, ур.2.18]
dФр/dT = -D(d2Фр/dT2)/
Здесь D – коэффициент пропорциональности. Этот подход мало информативен, поэтому далее он не рассматривается.
2). Термодинамический подход. Рассматривая физическую природу этих уравнений, прежде всего заметим, что «фракция» означает относительное количество выделившегося вещества, т.е. если абсолютное количество выделившегося вещества – n, а всего навеса – N, то величина фракции Фр = n·100/N. В грубом приближении можно принять, что величина n/N соответствует величинам коэффициентов распределения
|
Месторождение
|
Воз-раст
|
ToC
|
ΔHо,
ккал
|
Фo, %
|
Регион
|
Исто-чник
|
|
|
Супса.
|
N
|
194,3
|
2,641
|
13
|
Грузия
|
[6]
|
|
|
Чаладиди.
|
K
|
420,3
|
1,764
|
9
|
Грузия
|
[6]
|
|
|
Озек-Суэт, скв.69. да.
|
K
|
539,4
|
3,237
|
10
|
Ставрополье
|
[4]
|
|
|
Озек-Суэт, скв.69. па.
|
K
|
547,1
|
3,126
|
16
|
Ставрополье
|
[4]
|
|
|
Озек-Суэт, скв.42. да.
|
J
|
525,5
|
2,700
|
9
|
Ставрополье
|
[4]
|
|
|
Озек-Суэт, скв.42. па.
|
J
|
327,8
|
2,103
|
11
|
Ставрополье
|
[4]
|
|
|
Назинская нефть.
|
J
|
384,5
|
2,573
|
24
|
З. Сибирь.
|
[5]
|
|
|
Назинская нефть.
|
J
|
499,3
|
2,839
|
11
|
З. Сибирь.
|
[5]
|
|
|
Зольный Овраг, скв.3.
|
C
|
477,7
|
2,792
|
9
|
Волго-Урал.
|
[3]
|
|
|
Красноярка, скв. 42.
|
C
|
137,7
|
2,016
|
9
|
Волго-Урал.
|
[3]
|
|
|
Красноярка, скв. 41.
|
C
|
261,8
|
2,129
|
10
|
Волго-Урал.
|
[3]
|
|
|
Краснокамское, табл.159.
|
C
|
246,95
|
2,594
|
5
|
Волго-Урал.
|
[9]
|
|
|
Зольный Овраг, скв. 87.
|
D
|
100,5
|
1,999
|
10
|
Волго-Урал.
|
[3]
|
|
|
Брусиловский.
|
-
|
119(122)*
|
2,200
|
15
|
-
|
[10]
|
|
|
Примечание: звёздочкой отмечены значения пластовой температуры.
|
|||||||
выделившихся компонентов, условно равных отношениям их мольных долей. Они отражают состояние термодинамического равновесного распределения возгонов между остаточной нефтью и воздухом. В петрологии и физической химии известен вид распределения примеси между расплавом и кристаллической фазой. Один из них представлен уравнением [14] ln(Nl/Nc) = (-ΔHпл/R)(1/T - 1/Tпл), где Nl и Nc– мольные доли примеси в расплавленной и кристаллической фазах, ΔHпл и Tпл – соответственно теплота и температура плавления растворителя, Т - текущая температура [14]. Это уравнение не совсем соответствует уравнению (8). Главное отличие заключается в наличии квадрата температуры в (8). Ближе всего к этой ситуации приближаются уравнения фракционирования изотопов лёгких элементов , C и пр.). Об этом говорилось во Введении. Заметим, что сравнение обусловлено аналогией в распределении примеси между расплавом и кристаллом с одной стороны и, как в нашем случае, распределение примеси (возгона) между жидким веществом (нефтью) и газом (воздухом). Эта аналогия и позволила использовать результаты термодинамических исследований в системе жидкость- кристалл. С учётом этих данных, а также соблюдения принципов размерности выражение (8) можно представить в виде уравнения
ln(Фр/100) – ln(Фро/100) ≈ -[(ΔHi/R)2 (1/T – 1/То)2], (9)
где ΔHi– возможная истинная энтальпия (растворения) возгона нефтяного вещества, т.е. теплота астворения примеси, выделяемой в виде возгона, Фро – количество фракции, выделившейся при То. Принято, что В = ln(Фро/100). На рис. 8 показано распределение термодинамических параметров нефтей с возрастом. Более – менее чётко проявлено изменение параметра To, величина которого уменьшается с возрастом. Такая же тенденция наблюдается и в изменении параметра ΔHо. В обоих случаях наибольшие значения параметров характерны для нефтей среди меловых отложений.
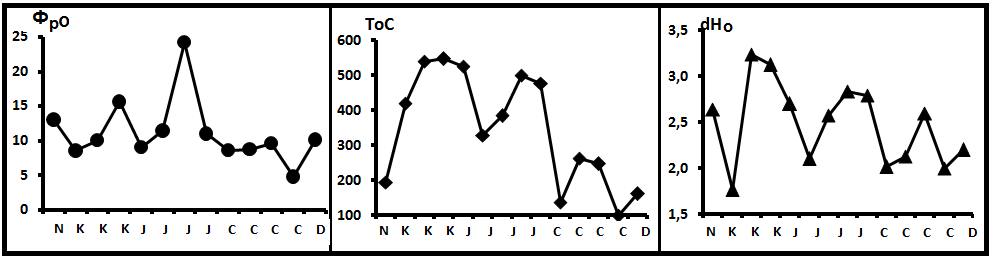
Рис. 8. Поведение термодинамических параметров с возрастом.
В табл. 3 приведены результаты определения термодинамическихпараметров возгонов. Согласно им максимальная температура растворения достигает ~550оС. На рис.9 показан характер совместного поведения ТоС и ΔHо. Для сравнения сюда же помещены данные по техническому маслу СО - 100. На графике латинскими буквами отмечен возраст пород, вмещающих нефть. По этим данным отмечается положительная связь между этими
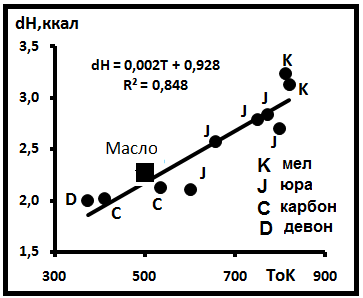
Рис.9. Диаграмма совместного поведения ТоK и DHо.
параметрами в течение всего времени существования нефти. Это говорит о примерном постоянстве во времени отношения ΔH/T. В свою очередь это отношение имеет размерность энтропии, что позволяет предложить равенство ΔSр ≈ 2 кал/(М• К) = 8,334 Дж/(М• К) и отметить её примерное постоянство во времени в изученном пространстве параметров.
Заключение.
Рассмотрено поведение нефти при воздействии на неё высоких температур в экспериментальных условиях (возгоны нефти) и установлено, что в значительном количестве случаев её распределение описывается полиномом второй степени. Это распределение отождествляется с параболическим уравнением вида y = Ax2 + Bx + C. В семействе параболических уравнений, т.е. уравнений, описывающих распределение параметров вещества одного и того же состава в разных природных условиях, их параметры описываются уравнениями прямой линии B = mA + M и C = kA + K (надкомпенсационные уравнения). Для нефтей эти уравнения приобретают вид B = -4,089A - 0,489 и C= 3,996A - 1,629. Физический смысл этих надкомпенсаций не ясен. Интерпретация полиномов опирается на изученные в петрологии представления о распределении примеси между двумя веществами; в данном случае возгон параллелезуется с примесью некоторого вещества. В этом случае распределение возгонов описывается уравнением
ln(Фр/100) – ln(Фро/100) ≈ -[(DHi/R)2 (1/T – 1/То)2],
где Фр - величина фракции при температуре ToK, DHi – теплота растворения примеси в нефти. Расчёты показали, что параметры распределений колеблются в пределах: То = 100 – 550оК, DH =1,764 – 2,237 ккал/Моль, Фро = 5 - 24%. Выявлена статистически положительная связь ТоК и DH, причем с возрастом значения пары уменьшаются.
Литература:
1.Макаров В.П. Нефть. Новые данные об её составе. / Международная научно-практическая конференция «Научные исследования и их практическое применение. Современное состояние и пути развития ‘2013». //Одесса: изд-во Куприенко С.В., 2013, Т.51. С. 71 - 77.
URL: sworld.com.ua›konfer32/90.pdf. http://www.lithology.ru/node/926.
2.Макаров В.П. Нефть. Основные свойства (сводные данные)./Материалы международного симпозиума «Перспективные тренды развития науки: медицина и фармацевтика, биология, география и геология». Глава 4. Одесса: изд-во Куприенко С.В., 2016. С.78-100. URL: http://www.sworld.com.ua/index.php/ru/c216-13/28011-с216-002.DOI:10.21893/978-966-2769-7.0.
3.Котина А. К., Чихачева Е. М. Групповой состав нефтей Волго-Уральской области с учетом в них сернистых соединений. /Геологический сборник, №1. Л.: Гостоптехиздат. 1955. С.454-465.
4. Котина А.К., Чихачева Е.М. Исследование нефтей месторождения Озек-Суат. // Геохимический сборник. №7. Труды ВНИГРИ, вып.174. Л.: Гостоптехиздат, 1961, С. 35-53.
5. Богомолов А. И., Стригалева Н. В. , Панина К. И. Назинская нефть Западной Сибири. //Геохимический сборник №6,вып. 155, 1960. С.85 – 89.
6. Мишунина З.А. Карбонатные формации и их нефтепроизводящие свиты. Условия формирования карбонатных формаций. /Нефтепроизводящие свиты карбонатных формаций. Труды ВНИГРИ, вып.271. Л.: Недра, 1971. 263 с.
7. Поляков В.Б. Новые калибровки углеродных и кислородных изотопных геотермометров (карбонаты, графит, магнетит). URL:http://geo.web.ru/conf/alkaline/2007/62.pdf.
8.Макаров В.П. Методические вопросы геологии. О грубых ошибках в решении геологических задач. / Международная научно-практическая конференция «Перспективные инновации в науке, образовании, производстве и транспорте’2013». Одесса: изд-во Куприенко С.В., 2013, Т.53. С.71 – 94. URL: http://www.литология.рф/node/937.
9. Борисов А. А., Бочков И. В., Васильев Г. И. и др. Урало-Волжская нефтеносная область (Геология и нефтеносность). М.-Л.: Гостоптехиздат, 1941.
10.Брусиловский А.И. Фазовые превращения при разработке месторождений нефти и газа. М.: Изд. дом «Грааль», 2002. 575 с.
11. Макаров В.П. Явление компенсации» - новый вид связи между геологическими объектами. / Материалы I Международной научно- практической конференции «Становление современной науки – 2006». Днепропетровск, 2006. т.10, стр. 85- 115. URL: http://www.литология.рф/node/817.
12. Бухмиров В.В., Ракутина Д.В., Солнышкова Ю.С. Справочные материалы для решения задач по курсу «Тепломассообмен». Иваново: Ивановский государственный энергетический университет, 2009.
14. Макаров В.П. К теории геохимических геотермометров. 3. Новая интерпретация параметров уравнения геотермометра. /"Вестник отделения наук о земле РАН". Электронный научно-информационный журнал, № 1(24)' 2006. URL: http://www.scgis.ru/russian/cp1251/h_dgggms/1-2006/informbul-1_2006/term-22.pdf.
15. Чупров И. Ф., Канева Е. А. Уравнения параболического типа и некоторые методы их решения. Ухта: УГТУ, 2012. URL: ib.ugtu.net›system/files/books/2012…i…uravneniya…
Примечание: Источник информации: Макаров В.П. и др. Перспективные тренды развития науки: Медицина и Фарматевтика, Биология, География и геология. Монография. Одесса:изд.Куприенко С.В. 2016. С.
- Войдите или зарегистрируйтесь, чтобы получить возможность отправлять комментарии